题目内容
3.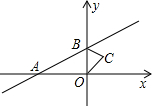 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).
分析 首先解得点A和点B的坐标,再利用位似变换可得结果.
解答 解:∵直线y=x+1与x轴交于点A,与y轴交于点B,
令x=0可得y=1;
令y=0可得x=-1,
∴点A和点B的坐标分别为(-1,0);(0,1),
∵△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,
∴$\frac{OB}{O′B′}$=$\frac{OA}{AO′}$=$\frac{1}{3}$,
∴O′B′=3,AO′=3,
∴B′的坐标为(-4,-3)或(2,3).
故答案为:(-4,-3)或(2,3).
点评 本题主要考查了位似变换和一次函数图象上点的坐标特征,得出点A和点B的坐标是解答此题的关键.

练习册系列答案
相关题目
14.若mn≠0,已知mx=nx,则下列结论成立的是( )
| A. | x=0 | B. | m,n一定相等 | C. | x=$\frac{n}{m}$ | D. | x的解不确定 |
18.已知二次函数y=-3(x-h)2+5,当x>-2时,y随x的增大而减小,则有( )
| A. | h≥-2 | B. | h≤-2 | C. | h>-2 | D. | h<-2 |
8. 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
(1)表中a、b、c、d分别为:a=78; b=56; c=0.18; d=0.28.
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?
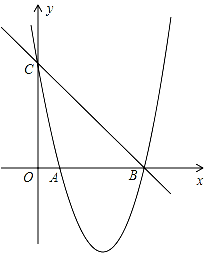 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5). 若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动,则直尺上的10cm刻度线对应量角器上的度数约为115°.(保留π)
若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动,则直尺上的10cm刻度线对应量角器上的度数约为115°.(保留π) 如图是2017年1月份的日历,在日历上任意圈出一个竖列上相邻的3个数.如果被圈出的三个数的和为63,则这三个数中最后一天为2017年1月28号.
如图是2017年1月份的日历,在日历上任意圈出一个竖列上相邻的3个数.如果被圈出的三个数的和为63,则这三个数中最后一天为2017年1月28号. 如图在直角坐标系中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,如果点M在y轴右侧的抛物线上,S△AMO=$\frac{2}{3}$S△COB,那么点M的坐标是(1,-6)或(4,6).
如图在直角坐标系中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,如果点M在y轴右侧的抛物线上,S△AMO=$\frac{2}{3}$S△COB,那么点M的坐标是(1,-6)或(4,6).