题目内容
6．某商场春节举行摸奖大酬宾活动，在第一个不透明的摸奖箱里放置了标号为A、B的两个红色球，在第二个不透明的摸奖箱里放置了标号为A、B、C的三个黄色球，在第三个不透明的摸奖箱里放置了标号为A、B、C、D的四个蓝色球，小球除了颜色、标号不同，其他均相同．（1）摸球一次，若摸到标号为A的球就可获奖，求获奖的概率．
（2）分别从三个摸奖箱各摸出一个球，若标号相同，则获得特等奖，球获得特等奖的概率．
分析 （1）根据概率公式求解可得；
（2）根据摸球步骤画出树状图列出所有等可能结果，再找到标号相同的结果数，由概率公式可得结果．
解答 解：（1）3个摸奖箱里共放置了9个小球，每一个小球被摸到的可能性是相同的，
因此摸到标号为A的球的概率是$\frac{3}{9}$=$\frac{1}{3}$，即获奖的概率为$\frac{1}{3}$；
（2）画树状图如下：
由树状图可知共有24种等可能结果，其中标号相同的有2种结果，
∴获得特等奖的概率为$\frac{2}{24}$=$\frac{1}{12}$．
点评 此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．
练习册系列答案
相关题目
如图，将一个长方形纸条折成如图的形状，若已知∠1=130°，则∠2=65°．
14．
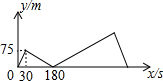甲、乙两人在直线道路上同起点，同终点，同方向，分别以不同的速度匀速跑步1500m，先到终点的人原地休息，已知甲先出发30s后，乙才出发，甲、乙两人的距离y（m）与甲出发的时间x（s）之间的关系如图所示，下列说法中错误的是（ ）
甲、乙两人在直线道路上同起点，同终点，同方向，分别以不同的速度匀速跑步1500m，先到终点的人原地休息，已知甲先出发30s后，乙才出发，甲、乙两人的距离y（m）与甲出发的时间x（s）之间的关系如图所示，下列说法中错误的是（ ）| A． | 甲的速度是2.5m/s，乙的速度为3m/s | |
| B． | 乙出发150秒后追上了甲 | |
| C． | 乙到达终点时，甲距终点250m | |
| D． | 甲到达终点比乙晚了70s |
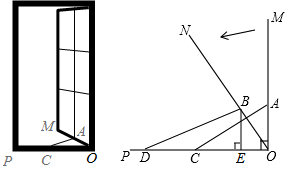
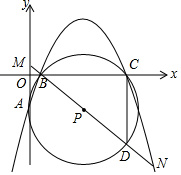已知：如图，抛物线y=ax2+bx+c与x轴相交于点B（1，0）和点C（9，0）两点，与y轴的负半轴相交于A点，过A、B、C三点的⊙P与y轴相切于点A，M为y轴正半轴上的一个动点，直线MB交⊙P于点D，交抛物线于点N．
11．抛物线y=x2+2x+m-1与x轴有交点，则m的取值范围是（ ）
| A． | m≤2 | B． | m＜-2 | C． | m＞2 | D． | 0＜m≤2 |
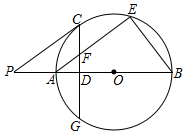如图，AB为⊙O的直径，AE是⊙O的弦，C是弧AE的中点，弦CG⊥AB于点D，交AE于点F，过点C作⊙O的切线，交BA延长线于点P，连接BE
15．
如图，正方形ABCD中，AB=2，E为BC中点，两个动点M和N分别在边CD和AD上运动且MN=1，若△ABE与以D、M、N为顶点的三角形相似，则DM为（ ）
如图，正方形ABCD中，AB=2，E为BC中点，两个动点M和N分别在边CD和AD上运动且MN=1，若△ABE与以D、M、N为顶点的三角形相似，则DM为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{1}{3}$或$\frac{2}{3}$ | D． | $\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$ |
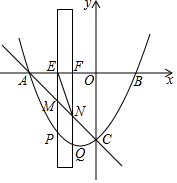如图，已知抛物线y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5与x轴交于A、B两点（点B在点A的右侧），与y轴交于点C，有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线AC于点M和点N，交x轴于点E和点F．