题目内容
1. 已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
分析 (1)过点P作PE⊥BC,垂足为E,连结AP.依据垂径定理可知BE=EC=4则OE=5,然后再证明四边形AOEP为矩形可求得到AP=OE=5,在Rt△BEP中,依据勾股定理可求得PE的长;
(2)设抛物线的解析式为y=a(x-1)(x-9),将点A的坐标代入求解即可;
(3)△MOB为直角三角形,则△BDC为直角三角形,故此只存在∠BCD为直角的情况,则MB经过点P,然后求得MB的解析式,将直线BM的解析式与抛物线的解析式组成方程组可求得点N的坐标,然后依据CD∥y轴可求得点CD的长,最后依据△CDN的面积=$\frac{1}{2}$DC•(xN-xD)求解即可.
解答 解:(1)如图1所示:过点P作PE⊥BC,垂足为E.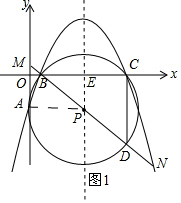
∵PE⊥BC,
∴BE=EC=4.
∴OE=5.
∵⊙P与y轴相切,
∴PA⊥y轴.
∵∠PAO=∠AOE=∠OEP=90°,
∴四边形AOEP为矩形.
∴AP=OE=5,AO=EP.
∴⊙P的半径为5.
在Rt△BEP中,PE=$\sqrt{B{P}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∴OA=3.
∴点A的坐标为(0,-3).
(2)设抛物线的解析式为y=a(x-1)(x-9),将点A的坐标代入得:9a=-3,解得a=-$\frac{1}{3}$,
∴抛物线的解析式为y=-$\frac{1}{3}$x2$+\frac{10}{3}$x-3.
(3)如图2所示:当直线MB经过点P时.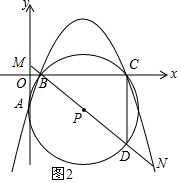
∵BD为⊙P的直径,
∴∠BCD=90°.
∴∠BCD=∠MOB=90°.
又∵∠MBO=∠CBD,
∴△MOB∽△DCB.
设MB的解析式为y=kx+b,将点B和点D的坐标代入得$\left\{\begin{array}{l}{k+b=0}\\{5k+b=-3}\end{array}\right.$,解得:k=-$\frac{3}{4}$,b=$\frac{3}{4}$.
∴直线MB的解析式为y=-$\frac{3}{4}$x+$\frac{3}{4}$.
将x=9代入得y=-6.
∴CD=6.
将y=-$\frac{3}{4}$x+$\frac{3}{4}$与y=-$\frac{1}{3}$x2$+\frac{10}{3}$x-3联立解得:x=1或x=$\frac{45}{4}$.
△CDN的面积=$\frac{1}{2}$DC•(xN-xD)=$\frac{1}{2}$×6×($\frac{45}{4}$-9)=$\frac{27}{4}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了,切线的性质、矩形的性质和判定、勾股定理、垂径定理的应用,待定系数法求一次函数的解析式,得到直线MB经过点P是解答本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | ±2 | C. | -2 | D. | 16 |
 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.
如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.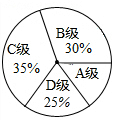 为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.
为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.