题目内容
17.如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm.(1)求B点到OP的距离;
(2)求滑动支架的长.(结果精确到0.1)
(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33)
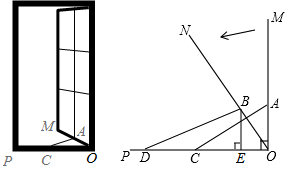
分析 (1)在Rt△BOE中,得到OE=$\frac{BE}{tan53°}$,在Rt△BDE中,得到DE=$\frac{BE}{tan28°}$,列方程即可得到结论;
(2)根据三角函数的定义即可得到结论.
解答 解:(1)在Rt△BOE中,OE=$\frac{BE}{tan53°}$,
在Rt△BDE中,DE=$\frac{BE}{tan28°}$,
则$\frac{BE}{tan53°}$+$\frac{BE}{tan28°}$=30,
解得BE≈11.4(cm).
故B点到OP的距离大约为11.4cm;
(2)在Rt△BDE中,BD=$\frac{BE}{sin28°}$≈24.2cm.
故滑动支架的长约为24.2cm.
点评 本题考查了解直角三角形的应用,正确的识别图形是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
8.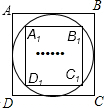 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )| A. | ($\frac{\sqrt{2}}{2}$)n | B. | ($\frac{1}{2}$)n | C. | ($\frac{\sqrt{3}}{2}$)n | D. | ($\frac{3}{4}$)n |
7.下列计算正确的是( )
| A. | x4+x2=x6 | B. | (a+b)2=a2+b2 | C. | (3x2y)2=6x4y2 | D. | (-m)7÷(-m)2=-m5 |
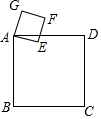 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.
如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm. 如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F.
如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F. 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.
如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.