题目内容
15. 如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )
如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$或$\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$ |
分析 根据勾股定理求出AE,分△ABE∽△MDN和△ABE∽△NDM两种情况,根据相似三角形的性质计算即可.
解答 解:∵E为BC中点,
∴BE=1,
由勾股定理得,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{5}$,
当△ABE∽△MDN时,$\frac{AB}{DM}$=$\frac{AE}{MN}$,即$\frac{2}{DM}$=$\frac{\sqrt{5}}{1}$,
解得,DM=$\frac{2\sqrt{5}}{5}$,
同理,当△ABE∽△NDM时,DM=$\frac{\sqrt{5}}{2}$,
∴DM为$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{2}$,
故选:D.
点评 本题考查的是相似三角形的性质、正方形的性质,掌握相似三角形的性质、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
7.下列计算正确的是( )
| A. | x4+x2=x6 | B. | (a+b)2=a2+b2 | C. | (3x2y)2=6x4y2 | D. | (-m)7÷(-m)2=-m5 |
4. 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )| A. | $\frac{2\sqrt{5}}{3}$ | B. | 1 | C. | $\frac{3\sqrt{17}}{17}$ | D. | $\frac{4\sqrt{17}}{17}$ |
19.已知∠AOB=30°,自∠AOB顶点O引射线OC,若∠AOC:∠AOB=4:3,那么∠BOC的度数是( )
| A. | 10° | B. | 40°或30° | C. | 70° | D. | 10°或70° |
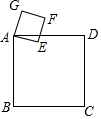 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.
如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.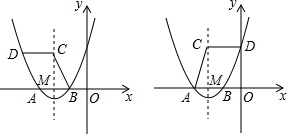
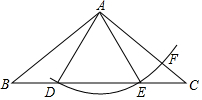 如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.
如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.