题目内容
3.在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上,记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=$(2+\sqrt{3})$:2,则下列四个结论:①AB:BE=$(2+\sqrt{3})$:2;②AE:BE=$\sqrt{3}$:2;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.正确的共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由矩形和菱形的面积关系得出AB:BE=$(2+\sqrt{3})$:2,①正确;AE:BE=$\sqrt{3}$:2,②正确;由菱形的性质得出DE∥BF,DE=BE,得出∠BFC=∠EDF,由三角函数求出∠ADE=60°,得出∠ADC=∠C=90°,求出∠EDF=30°,tan∠EDF=$\frac{\sqrt{3}}{3}$,③正确;∠BFC=30°,得出∠FBC=60°,④正确;即可得出结论.
解答 解:如图所示: ∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=$(2+\sqrt{3})$:2,
∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=$(2+\sqrt{3})$:2,
∴AB:BE=$(2+\sqrt{3})$:2,①正确;
∴AE:BE=$\sqrt{3}$:2,②正确;
∵四边形BFDE是菱形,
∴DE∥BF,DE=BE,
∴∠BFC=∠EDF,
∴sin∠ADE=$\frac{AE}{DE}$=$\frac{AE}{BE}$=$\frac{\sqrt{3}}{2}$,
∴∠ADE=60°,
∵∠ADC=∠C=90°,
∴∠EDF=90°-60°=30°,
∴tan∠EDF=$\frac{\sqrt{3}}{3}$,③正确;∠BFC=30°,
∴∠FBC=90°-30°=60°,④正确;
正确的共有4个;
故选:A.
点评 本题考查了矩形的性质、菱形的性质、三角函数等知识;熟练掌握矩形和菱形的性质,由矩形和菱形的性质得出AB:BE=$(2+\sqrt{3})$:2是解决问题的关键.

练习册系列答案
相关题目
14.点A(x1,y1)、B(x2,y2)是一次函数y=kx+2(k<0)图象上不同的两点,若t=(x2-x1)(y2-y1),则( )
| A. | t<0 | B. | t=0 | C. | t>0 | D. | t≤0 |
13.在Rt△ABC中,∠C=90°,BC=6,AC=8,则cos∠BAC等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
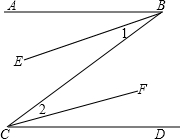 在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.
在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.