题目内容
14．点A（x1，y1）、B（x2，y2）是一次函数y=kx+2（k＜0）图象上不同的两点，若t=（x2-x1）（y2-y1），则（ ）| A． | t＜0 | B． | t=0 | C． | t＞0 | D． | t≤0 |
分析 根据一次函数的性质分两种情况进行讨论：①若x1＞x2，则y1＜y2；②若x1＜x2，则y1＞y2．
解答 解：∵一次函数y=kx+2中k＜0，
∴此函数是减函数．
①若x1＞x2，则y1＜y2，
故x1-x2＞0，y1-y2＜0，
所以t＜0；
②若x1＜x2，则y1＞y2，
因此x1-x2＜0，则y1-y2＞0，
故t＜0；
故选A．
点评 此题考查的是一次函数图象上点的坐标特点，关键是掌握一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
4．若直线y1=m2x+a与直线y2=-2x+b的交点坐标为（1，2），则使y1＜y2成立的x的取值范围为（ ）
| A． | x＞1 | B． | x＞2 | C． | x＜1 | D． | x＜2 |
设△ABC是锐角三角形，∠A，∠B所对的边长分别为a、b，其边上的高分别为m，n，∠ACB=θ．
如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在y轴上，点B1，B2，B3，…都在直线y=$\frac{\sqrt{3}}{3}$x上，则点A2的坐标是（2$\sqrt{3}$，4）．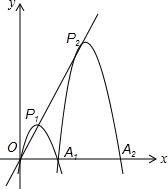
已知在平面直角坐标系xOy中，抛物线y1=ax2+bx（a≠0），与x轴正半轴交于点A1（2，0），顶点为P1，△OP1A1为正三角形，现将抛物线y1=ax2+bx（a≠0）沿射线OP1平移，把过点A1时的抛物线记为抛物线y2，记抛物线y2与x轴的另一交点为A2；把抛物线y2继续沿射线OP1平移，把过点A2时的抛物线记为抛物线y3，记抛物线y3与x轴的另一交点为A3；…．；把抛物线y2015继续沿射线OP1平移，把过点A2015时的抛物线记为抛物线y2016，记抛物线y2016与x轴的另一交点为A2016，顶点为P2016．若这2016条抛物线的顶点都在射线OP1上．