题目内容
3.解方程组:$\left\{\begin{array}{l}{\frac{x}{7}=\frac{y}{10}=\frac{z}{5}}\\{x+2y+3z=84}\end{array}\right.$.分析 令第一个方程等于k,表示出x,y,z,代入第二个方程求出k的值,即可确定出方程组的解.
解答 解:令$\frac{x}{7}$=$\frac{y}{10}$=$\frac{z}{5}$=k,可得x=7k,y=10k,z=5k,
代入x+2y+3z=84中,得:7k+20k+15k=84,即k=2,
则x=2k=14,y=10k=20,z=5k=10.
则方程组的解为$\left\{\begin{array}{l}{x=14}\\{y=20}\\{z=10}\end{array}\right.$.
点评 此题考查了解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.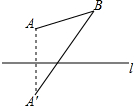 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )| A. | A′B2-AB2=13 | B. | A′B2-AB2=24 | C. | A′B2+AB2=25 | D. | A′B2+AB2=26 |
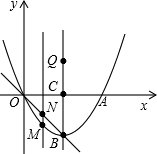 如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.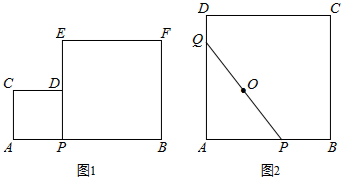
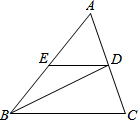 如图,在△ABC中,BD交AC于点D,DE交AB于点E,∠EBD=∠EDB,∠ABC:∠A:∠C=5:6:7,∠BDC=85°.
如图,在△ABC中,BD交AC于点D,DE交AB于点E,∠EBD=∠EDB,∠ABC:∠A:∠C=5:6:7,∠BDC=85°.