题目内容
18.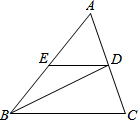 如图,在△ABC中,BD交AC于点D,DE交AB于点E,∠EBD=∠EDB,∠ABC:∠A:∠C=5:6:7,∠BDC=85°.
如图,在△ABC中,BD交AC于点D,DE交AB于点E,∠EBD=∠EDB,∠ABC:∠A:∠C=5:6:7,∠BDC=85°.(1)求∠BED的度数;
(2)ED与BC有怎样的位置关系?为什么?
分析 (1)根据已知和三角形内角和定理求出∠A=50°,∠ABC=60°,∠C=70°,根据三角形内角和定理求出∠DBC=180°-∠C-∠BDC=25°,代入求出∠EBD=∠EDB=∠ABC-∠DBC=25°,根据三角形内角和定理得出∠BED=180°-∠EBD-∠EDB,代入求出即可;
(2)求出∠EDB=∠DBC,根据平行线的判定得出即可.
解答 解:(1)∵∠ABC:∠A:∠C=5:6:7,∠ABC+∠A+∠C=180°,
∴∠A=50°,∠ABC=60°,∠C=70°,
∵∠BDC=85°,
∴∠DBC=180°-∠C-∠BDC=25°,
∴∠EBD=∠EDB=∠ABC-∠DBC=50°-25°=25°,
∴∠BED=180°-∠EBD-∠EDB=180°-25°-25°=130°;
(2)ED∥BC,
理由是:∵∠EDB=25°,∠DBC=25°,
∴∠EDB=∠DBC,
∴ED∥BC.
点评 本题考查了三角形的内角和定理,平行线的判定的应用,解此题的关键是求出各个角的度数,注意:内错角相等,两直线平行.

练习册系列答案
相关题目
9.一个多边形的每个内角都等于120°,则此多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
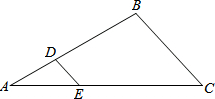 如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.
如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.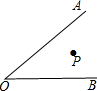 根据下列要求画图.
根据下列要求画图.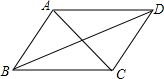 如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)
如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)