题目内容
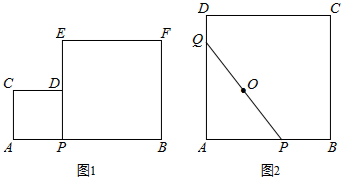
17.某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
(1)在点P运动时,这两个正方形面积之和是定值吗?如果时求出;若不是,求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
分析 (1)设AP=x,则PB=8-x,求出正方形APDC与正方形PBFE的面积之和=x2+(8-x)2=2(x-4)2+32,得出当x=4时,这两个正方形面积之和有最小值,最小值为32;
(2)设AP=a,则PB=BF=8-a.由平行线得出比例式 $\frac{PK}{BF}=\frac{AP}{AB}$,得出PK、DK,求出△APK和△DFK的面积,即可得出结论;
(3)根据题意得出:点O在以A为圆心,半径为4,圆心角为90°的圆弧上;得出PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,由弧长公式即可得出结果.
解答 解:(1)当点P运动时,这两个正方形的面积之和不是定值;理由如下:
设AP=x,则PB=8-x,
根据题意得:正方形APDC与正方形PBFE的面积之和=x2+(8-x)2=2(x-4)2+32,
∴当x=4时,这两个正方形面积之和有最小值,最小值为32;
(2)存在两个面积始终相等的三角形,它们是△APK与△DFK;理由如下:
依题意画出图形,如图1所示: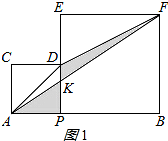
设AP=a,则PB=BF=8-a.
∵PE∥BF,
∴△APK∽△ABF,
∴$\frac{PK}{BF}=\frac{AP}{AB}$,
即 $\frac{PK}{8-a}=\frac{a}{8}$,
∴PK=$\frac{a(8-a)}{8}$,
∴DK=PD-PK=a-$\frac{a(8-a)}{8}$=$\frac{{a}^{2}}{8}$,
∴S△APK=$\frac{1}{2}$PK•PA=$\frac{1}{2}$•$\frac{a(8-a)}{8}$•a=$\frac{{a}^{2}(8-a)}{16}$,
S△DFK=$\frac{1}{2}$DK•EF=$\frac{1}{2}$•$\frac{{a}^{2}}{8}$•(8-a)=$\frac{{a}^{2}(8-a)}{16}$,
∴S△APK=S△DFK;
(3)当点P从点A出发,沿A→B→C→D的线路,向点D运动时,不妨设点Q在DA边上,
若点P在点A,点Q在点D,此时PQ的中点O即为DA边的中点;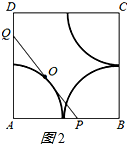 若点Q在DA边上,且不在点D,则点P在AB上,且不在点A;
若点Q在DA边上,且不在点D,则点P在AB上,且不在点A;
此时在Rt△APQ中,O为PQ的中点,
∴AO=$\frac{1}{2}$PQ=4;
∴点O在以A为圆心,半径为4,圆心角为90°的圆弧上;
PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如图2所示:
∴PQ的中点O所经过的路径的长为:$\frac{3}{4}$×2π×4=6π.
点评 本题是四边形综合题目,考查了正方形面积的计算、二次函数的最小值、相似三角形的判定与性质、三角形面积的计算、弧长公式、点和圆的位置关系等知识;本题难度较大,综合性强,特别是(2)、(3)中,需要通过证明三角形相似和判定点和圆的位置关系才能得出结果.

| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 4 | 2 | 2 | 1 |
| A. | 平均数是38.5 | B. | 众数是4 | C. | 中位数是40 | D. | 极差是3 |
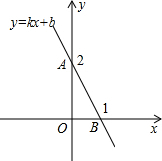 如图,直线y=kx+b经过点A,B,则不等式kx+b<0的解集是( )
如图,直线y=kx+b经过点A,B,则不等式kx+b<0的解集是( )| A. | x>1 | B. | x<1 | C. | x<0 | D. | 0<x<1 |
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
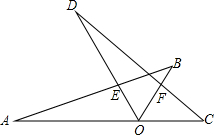 如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求: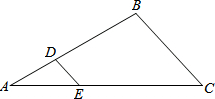 如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.
如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.