题目内容
11.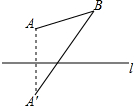 如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )
如图,A,B是直线l同侧的两点,作点A关于直线l的对称点A′,连结A′B.若点A,B到直线l的距离分别为2和3,则线段AB与A′B之间的数量关系是( )| A. | A′B2-AB2=13 | B. | A′B2-AB2=24 | C. | A′B2+AB2=25 | D. | A′B2+AB2=26 |
分析 连接A′A,作BF⊥l交l的平行线A′F于F,作A′K⊥BF,垂足为K.构造直角三角形,用勾股定理解答.
解答 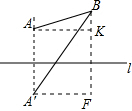 解:如图,连接A′A,作BF⊥l交l的平行线A′F于F,作A′K⊥BF,垂足为K.
解:如图,连接A′A,作BF⊥l交l的平行线A′F于F,作A′K⊥BF,垂足为K.
在Rt△A′FB中,A′B2=BF2+A′F2,
即A′B2=25+A′F2,
∵在Rt△AKB中,AK2=AB2-BK2,
又∵AK=A′F,
于是,A′B2=25+AB2-BK2,
即A′B2=25+AB2-1,
∴A′B2-AB2=24,
故选B.
点评 本题考查了勾股定理,构造直角三角形,灵活运用勾股定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表.关于这10户家庭的月用电量说法正确的是( )
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 4 | 2 | 2 | 1 |
| A. | 平均数是38.5 | B. | 众数是4 | C. | 中位数是40 | D. | 极差是3 |
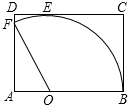 如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.
如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.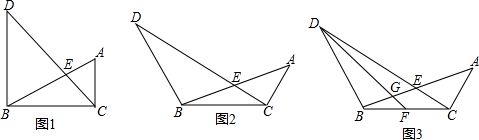
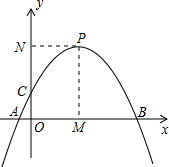 如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.
如图,开口向下的抛物线y=a(x-2)2+k,交x轴于点A、B(点A在点B左侧),交y轴正半轴于点C,顶点为P,过顶点P,作x轴,y轴的垂线,垂足分别为M,N.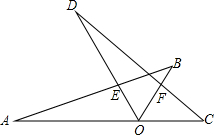 如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求: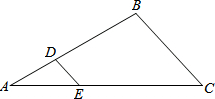 如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.
如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.