题目内容
12.在△ABC中,AB=AC,直线MN垂直平分AB交AB于D点,交AC所在的直线与E点,若∠AED=40°,则∠EBC=15°或75°.分析 根据题意画出符合条件的两种情况,求出∠ABE,∠ABC,根据角的和差得到∠CBE,即可求出答案.
解答 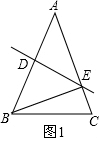 解:
解:
分为两种情况:①如图1,
∵DE垂直平分AB,
∴∠ADE=90°,
∵∠AED=40°,
∴∠A=180°-90°-40°=50°,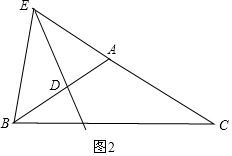
∴∠ABE=∠A=50°,
∵AB=AC,
∴∠ABC=65°,
∴∠EBC=15°;
②如图2,
∵DE垂直平分AB,
∴∠ADE=90°,
∵∠AED=40°,
∴∠EAD=180°-90°-40°=50°,
∴∠BAC=180°-50°=130°,
∴∠EAB=∠EBA=50°,∠B=∠C=25°,
∴∠EBC=75°,
故答案为:15°或75°.
点评 本题考查了等腰三角形的性质和线段垂直平分线性质,三角形的内角和定理,解此题的关键是能求出符合条件的所有情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
 有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )
有理数a,b在数轴上的位置如图所示,在-a,b-a,a+b,0中,最大的是( )| A. | -a | B. | 0 | C. | a+b | D. | b-a |
20.在平面直角坐标系中,二次函数y=x2+ax+b的图象与x轴交于两点,且两交点之间的距离是4,若此函数图象的对称轴为x=-5,则此图象经过下列( )
| A. | (-6,-4) | B. | (-6,-3) | C. | (-6,-2) | D. | (-6,-1) |
2.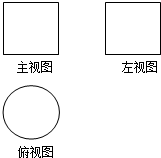 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
 如图,EF∥AD,∠1=∠2,∠BAC=75°.
如图,EF∥AD,∠1=∠2,∠BAC=75°.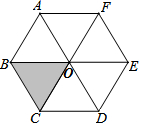 如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.
如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.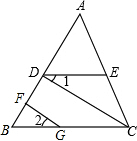 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.