题目内容
6. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵AE=DE,
∴S△BDE=S△ABE,S△CDE=S△ACE,
∴S△BDE=$\frac{1}{2}$S△ABD,S△CDE=$\frac{1}{2}$S△ACD,
∴S△BCE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×36=18(cm2);
∵EF=CF,
∴S△BEF=S△BCF,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×18=9(cm2),
即△BEF的面积是9cm2,
故答案为:9cm2.
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
相关题目
18.若式子$\sqrt{k-1}$+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.下列说法错误的是( )
| A. | 斜边及一锐角分别相等的两个直角三角形全等 | |
| B. | 两条直角边分别相等的两个直角三角形全等 | |
| C. | 两个锐角分别相等的两个直角三角形全等 | |
| D. | 一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等 |

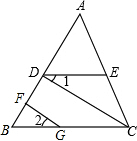 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.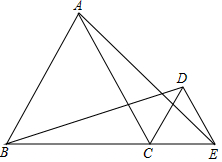 如图,△ABC,△CDE是等边三角形.
如图,△ABC,△CDE是等边三角形.