题目内容
19.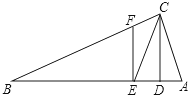 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.(1)CD与EF平行吗?并说明理由;
(2)若∠A=70°,求∠FEC的度数.
分析 (1)根据垂直的定义可得∠CDB=∠FEB,可证明EF∥CD;
(2)在Rt△ADC中可求得∠ACD,再结合角平分线的定义可求得∠ECD,再由(1)根据平行线的性质可求得∠FEC.
解答 (1)证明:
∵CD⊥AB,EF⊥AB,
∴∠CDB=∠FEB=90°,
∴EF∥CD;
(2)解:
∵∠ACB=90°,CE平分∠ACB交AB于E,
∴∠ACE=45°,
∵∠A=70°,
∴∠ACD=90°-70°=20°,
∴∠ECD=∠ACE-∠ACD=25°,
∵EF∥CD,
∴∠FEC=∠ECD=25°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角相等?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
4.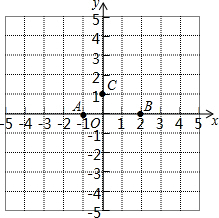 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
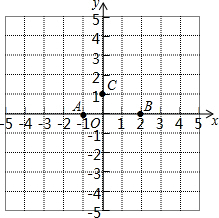 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )| A. | (3,1) | B. | (-4,1) | C. | (1,-1) | D. | (-3,1) |
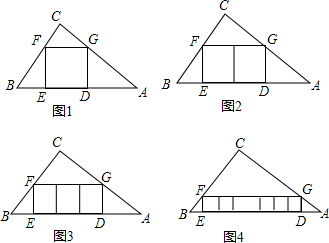
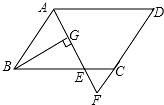 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求: