题目内容
11.已知一次函数y=(m-2)x-3m2+12,问:(1)m为何值时,函数图象过原点?
(2)m为何值时,函数图象平行于直线y=2x?
(3)m为何值时,函数图象过点(0,-15),且y随x的增大而减小?
分析 (1)图象经过原点,该函数为正比例函数,据此求解;
(2)当比例系数相同时两条直线平行;
(3)根据经过的点的坐标求得m的值,然后根据其增减性进行取舍即可.
解答 解:(1)∵一次函数图象经过原点
∴-3m2+12=0且m-2≠0,
∴m=-2;
(2)∵函数图象平行于直线y=2x,
∴m-2=2,
解得m=4;
(3)把(0,-15)代入解析式,得-3m2+12=-15,
解得m=±3,
又∵y随x的增大而减小,
∴m-2<0即m<2
∴m=-3.
点评 本题考查了一次函数的性质.一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.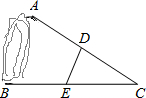 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )| A. | 280米 | B. | 300米 | C. | 420米 | D. | 无法确定 |
16.下列运算正确的是( )
| A. | x2+x3=x5 | B. | a3•a4=a12 | C. | (2x)4=8x4 | D. | (-x3y)2=x6y2 |
20. 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{5}$ |
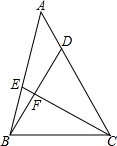 如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.
如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.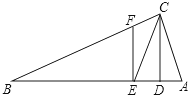 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.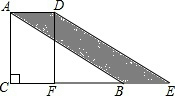 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )