题目内容
9.已知x2=4,(y+1)3-3=$\frac{3}{8}$,且x>y,则$\frac{x}{y}$的平方根为±2.分析 先根据平方根、立方根的定义求出x,y的值,再根据平方根的定义,即可解答.
解答 解:x2=4,
x=±2,
(y+1)3-3=$\frac{3}{8}$,
$(y+1)^{3}=\frac{27}{8}$,
y=$\frac{1}{2}$,
∵x>y,
∴x=2,y=$\frac{1}{2}$,
∴$\frac{x}{y}=\frac{2}{\frac{1}{2}}=4$
∴4的平方根为±2,
故答案为:±2.
点评 本题考查了平方根和立方根,解决本题的关键是熟记平方根、立方根的定义.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
20. 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{5}$ |
4. 若实数a,b,c在数轴上对应位置如图所示,则下列不等式成立的是( )
若实数a,b,c在数轴上对应位置如图所示,则下列不等式成立的是( )
 若实数a,b,c在数轴上对应位置如图所示,则下列不等式成立的是( )
若实数a,b,c在数轴上对应位置如图所示,则下列不等式成立的是( )| A. | ab>cb | B. | ac>bc | C. | a+c>b+c | D. | a+b>c+b |
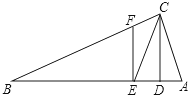 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.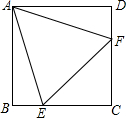 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( ) 如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.