��Ŀ����
8������ϸ�Ķ����ϣ��ٳ��Խ�����⣺��ȫƽ����ʽx2��2xy+y2=��x��y��2����x��y��2��ֵ��Ϊ�Ǹ������ص�����ѧѧϰ�����Ź㷺��Ӧ�ã�����̽�����ʽ2x2+12x-4�����С��ֵʱ�����ǿ�������������
�⣺ԭʽ=2��x2+6x-2��
=2��x2+6x+9-9-2��
=2[��x+3��2-11]
=2��x+3��2-22
��Ϊ����xȡʲô�������У�x+3��2��ֵΪ�Ǹ���
���ԣ�x+3��2����СֵΪ0����ʱx=-3
����2��x+3��2-22
����Сֵ��2��0-22=-22
���Ե�x=-3ʱ��ԭ����ʽ����Сֵ��-22
������⣺
���������Ľ���˼·��̽�����ʽ3x2-6x+12����Сֵ�Ƕ��٣���д����Ӧ��x��ȡֵ��
���� ԭʽ��ȡ3���䷽�����÷Ǹ��������������Сֵ���Լ���ʱx��ֵ���ɣ�
��� �⣺ԭʽ=3��x2-2x+4��
=3��x2-2x+1-1+4��
=3��x-1��2+9��
������xȡʲô�������У�x-1��2��ֵΪ�Ǹ�����
�ࣨx-1��2����СֵΪ0����ʱx=1��
��3��x-1��2+9����СֵΪ��3��0+9=9��
��x=1ʱ��ԭ����ʽ����Сֵ��9��
���� ���⿼������ȫƽ����ʽ���Ǹ��������ʣ��Լ��䷽����Ӧ�ã�����������ȫƽ����ʽ�ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
16������������ȷ���ǣ�������
| A�� | x2+x3=x5 | B�� | a3•a4=a12 | C�� | ��2x��4=8x4 | D�� | ��-x3y��2=x6y2 |
20�� ��ͼ����Rt��OAB�У�OA=2��AB=1��OA�������ϣ���O��ԭ���غϣ���ԭ��ΪԲ�ģ��߶�OB��Ϊ�뾶��������������������һ�㣬��������ʾ��ʵ���ǣ�������
��ͼ����Rt��OAB�У�OA=2��AB=1��OA�������ϣ���O��ԭ���غϣ���ԭ��ΪԲ�ģ��߶�OB��Ϊ�뾶��������������������һ�㣬��������ʾ��ʵ���ǣ�������
 ��ͼ����Rt��OAB�У�OA=2��AB=1��OA�������ϣ���O��ԭ���غϣ���ԭ��ΪԲ�ģ��߶�OB��Ϊ�뾶��������������������һ�㣬��������ʾ��ʵ���ǣ�������
��ͼ����Rt��OAB�У�OA=2��AB=1��OA�������ϣ���O��ԭ���غϣ���ԭ��ΪԲ�ģ��߶�OB��Ϊ�뾶��������������������һ�㣬��������ʾ��ʵ���ǣ�������| A�� | $\sqrt{2}$ | B�� | $\sqrt{5}$ | C�� | 3 | D�� | 2$\sqrt{5}$ |
 ��ͼ��AB��CD������1=35�㣬���2�Ķ���Ϊ145�㣮
��ͼ��AB��CD������1=35�㣬���2�Ķ���Ϊ145�㣮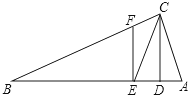 ��ͼ����ABC�У���ACB=90�㣬CD��AB��D��CEƽ�֡�ACB��AB��E��EF��AB��CB��F��
��ͼ����ABC�У���ACB=90�㣬CD��AB��D��CEƽ�֡�ACB��AB��E��EF��AB��CB��F�� ��ͼ����ƽ��ֱ������ϵ�У�����OABC�ĶԽ���ACƽ����x�ᣬ��OA��x��������ļн�Ϊ30�㣬OC=2�����C�������ǣ�-1��$\sqrt{3}$����
��ͼ����ƽ��ֱ������ϵ�У�����OABC�ĶԽ���ACƽ����x�ᣬ��OA��x��������ļн�Ϊ30�㣬OC=2�����C�������ǣ�-1��$\sqrt{3}$����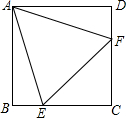 ��ͼ����������ABCD�У��߳�Ϊ2�ĵȱ�������AEF�Ķ���E��F�ֱ���BC��CD�ϣ����н��ۣ���CE=CF���ڡ�AEB=75�㣻��BE+DF=EF����AD=$\sqrt{3}$��������ȷ�Ľ��۸���Ϊ��������
��ͼ����������ABCD�У��߳�Ϊ2�ĵȱ�������AEF�Ķ���E��F�ֱ���BC��CD�ϣ����н��ۣ���CE=CF���ڡ�AEB=75�㣻��BE+DF=EF����AD=$\sqrt{3}$��������ȷ�Ľ��۸���Ϊ��������