题目内容
 如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE.
如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE.(1)求证:△ACD≌△BCE;
(2)若BC=8时,求点C到直线BE的距离.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证AC=BC,CD=CE,∠ACB=∠DCE=60°,可得∠ACD=∠BCE,即可证明△ACD≌△BCE;
(2)易证BO=CO,CO⊥AD,即可求得CO=4,可得点C到AD距离为4,根据△ACD≌△BCE,即可解题.
(2)易证BO=CO,CO⊥AD,即可求得CO=4,可得点C到AD距离为4,根据△ACD≌△BCE,即可解题.
解答:(1)证明:∵△ABC、△DCE为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD+∠BCD=60°,∠BCD+∠BCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE,(SAS);
(2)解:∵△ABC是等边三角形,AO是∠BAC的角平分线,
∴BO=CO,CO⊥AD,
∵BC=8,
∴CO=4,
∴点C到AD距离为4,
∵△ACD≌△BCE,
∴点C到直线BE的距离为4.
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD+∠BCD=60°,∠BCD+∠BCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE,(SAS);
(2)解:∵△ABC是等边三角形,AO是∠BAC的角平分线,
∴BO=CO,CO⊥AD,
∵BC=8,
∴CO=4,
∴点C到AD距离为4,
∵△ACD≌△BCE,
∴点C到直线BE的距离为4.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考察了等边三角形的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
余姚中学有甲、乙、丙、丁四门选修课,每人每周能选上一周没选的三门课之一,若一同学第一周选修甲,则第五周选修甲的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于
如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于 如图,点M(3,m)和点N(2,n)分别在抛物线y=
如图,点M(3,m)和点N(2,n)分别在抛物线y=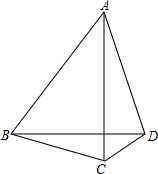 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°. 如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点.若CE的长为2π,BC=8+4
如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点.若CE的长为2π,BC=8+4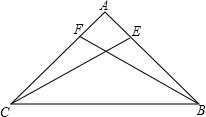 在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗?
在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗? 作图题:如图所示是每一个小方格都是边长为1的正方形网格,
作图题:如图所示是每一个小方格都是边长为1的正方形网格,