题目内容
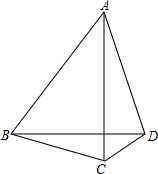 已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.(1)试探究BD、DC与AB之间的数量关系.
(2)证明你的结论.
考点:全等三角形的判定与性质
专题:
分析:延长BD至E,使BE=AB,连接AE、CE,可得△ABE是等边三角形,即可求得AC=AE,可得∠ACE=∠AEC,即可求得∠DCE=∠DEC,可得DE=CD,即可解题.
解答:证明:(1)AB=BD+CD;
(2)延长BD至E,使BE=AB,连接AE、CE,
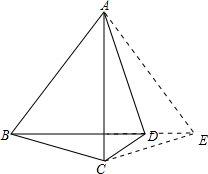
∵∠ABD=60°,
∴△ABE是等边三角形,
∴AE=AB,∠AEB=60°,
∵AB=AC,
∴AC=AE,
∴∠ACE=∠AEC,
∵∠ACD=60°,
∴∠ACE-∠ACD=∠AEC-∠AEB,
即∠DCE=∠DEC,
∴DE=CD,
∴BE=BD+DE=BD+CD,
∴AB=BD+CD.
(2)延长BD至E,使BE=AB,连接AE、CE,

∵∠ABD=60°,
∴△ABE是等边三角形,
∴AE=AB,∠AEB=60°,
∵AB=AC,
∴AC=AE,
∴∠ACE=∠AEC,
∵∠ACD=60°,
∴∠ACE-∠ACD=∠AEC-∠AEB,
即∠DCE=∠DEC,
∴DE=CD,
∴BE=BD+DE=BD+CD,
∴AB=BD+CD.
点评:本题考查了等边三角形各内角为60°的性质,考查了等腰三角形的性质,本题中求证CD=DE是解题的关键.

练习册系列答案
相关题目
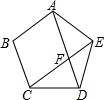 如图,正五边形ABCDE中,对角线AD、CE相交于F,求证:
如图,正五边形ABCDE中,对角线AD、CE相交于F,求证: 如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度.
如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度. 如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点.
如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点. 如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE.
如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE. 如图,AB=AC,∠1=∠2,AD=AE,则BD=
如图,AB=AC,∠1=∠2,AD=AE,则BD=