题目内容
 作图题:如图所示是每一个小方格都是边长为1的正方形网格,
作图题:如图所示是每一个小方格都是边长为1的正方形网格,(1)利用网格线作图:
①在BC上找一点P,使点P到AB和AC的距离相等;
②在射线AP上找一点Q,使QB=QC.
(2)在(1)中连接CQ与BQ,试说明△CBQ是直角三角形.
考点:作图—复杂作图,角平分线的性质,线段垂直平分线的性质
专题:
分析:(1)根据网格特点作出∠A的角平分线与BC的交点就是点P,作BC的垂直平分线与AP的交点就是点Q.
(2)首先利用勾股定理计算出CQ2、BQ2、BC2,然后利用勾股定理逆定理可得△CBQ是直角三角形.
(2)首先利用勾股定理计算出CQ2、BQ2、BC2,然后利用勾股定理逆定理可得△CBQ是直角三角形.
解答: 解:(1)点P就是所要求作的到AB和AC的距离相等的点,
解:(1)点P就是所要求作的到AB和AC的距离相等的点,
点Q就是所要求作的使QB=QC的点.
(2)连接CQ、BQ,
∵CQ2=12+52=26,BQ2=12+52=26,BC2=62+42=36+16=52,
∴CQ2+BQ2=BC2,
∴∠CQB=90°,
∴△CBQ是直角三角形.
 解:(1)点P就是所要求作的到AB和AC的距离相等的点,
解:(1)点P就是所要求作的到AB和AC的距离相等的点,点Q就是所要求作的使QB=QC的点.
(2)连接CQ、BQ,
∵CQ2=12+52=26,BQ2=12+52=26,BC2=62+42=36+16=52,
∴CQ2+BQ2=BC2,
∴∠CQB=90°,
∴△CBQ是直角三角形.
点评:本题主要考查了利用网格结构作角的平分线,线段的垂直平分线,关键是掌握角平分线的性质和线段垂直平分线的性质..

练习册系列答案
相关题目
 如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE.
如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE. 如图1,四边形ABCD中,AD=CD,∠BAD=∠BCD.
如图1,四边形ABCD中,AD=CD,∠BAD=∠BCD.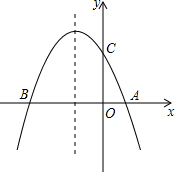 如图,抛物线y=-x2-2x+3于x轴交于A(1,0),B(-3,0)两点,交y轴于点C(0,3);在抛物线上是否存在点H,使得△BCH为直角三角形.
如图,抛物线y=-x2-2x+3于x轴交于A(1,0),B(-3,0)两点,交y轴于点C(0,3);在抛物线上是否存在点H,使得△BCH为直角三角形. 用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段a,c,∠α.
用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段a,c,∠α.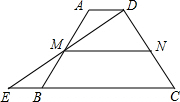 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M