题目内容
 如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于
如图,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=4,AC=3,内接矩形PQMN的周长等于| 47 |
| 6 |
考点:相似三角形的判定与性质,矩形的性质
专题:
分析:求出BC、AD的长度;证明△APN∽△ABC,列出比例式求出PN与PQ之间的数量关系;借助周长求出PN、PQ的长度,即可解决问题.
解答: 解:如图,由勾股定理得:BC2=AB2+AC2,
解:如图,由勾股定理得:BC2=AB2+AC2,
∵AB=4,AC=3,
∴BC=5;
由面积公式得:AB•AC=BC•AD,
∴AD=
=2.4.
∵四边形PQMN是矩形,AD⊥BC,
∴PQ=ED(设为λ),AE=AD-λ,PN∥BC,
∴△APN∽△ABC,
∴
=
,即
=
,
∴PN=5-
λ;
∵矩形PQMN的周长等于
,
∴2λ+2(5-
λ)=
,
解得:λ=1,
∴矩形PQMN的面积=1×(5-
)=
.
故答案为:
.
 解:如图,由勾股定理得:BC2=AB2+AC2,
解:如图,由勾股定理得:BC2=AB2+AC2,∵AB=4,AC=3,
∴BC=5;
由面积公式得:AB•AC=BC•AD,
∴AD=
| 12 |
| 5 |
∵四边形PQMN是矩形,AD⊥BC,
∴PQ=ED(设为λ),AE=AD-λ,PN∥BC,
∴△APN∽△ABC,
∴
| PN |
| BC |
| AE |
| AD |
| PN |
| 5 |
| 2.4-λ |
| 2.4 |
∴PN=5-
| 25 |
| 12 |
∵矩形PQMN的周长等于
| 47 |
| 6 |
∴2λ+2(5-
| 25 |
| 12 |
| 47 |
| 6 |
解得:λ=1,
∴矩形PQMN的面积=1×(5-
| 25 |
| 12 |
| 35 |
| 12 |
故答案为:
| 35 |
| 12 |
点评:该题主要考查了矩形的性质、相似三角形的判定及其性质定理的应用问题;牢固掌握定理是灵活解决问题的基础和关键.

练习册系列答案
相关题目
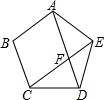 如图,正五边形ABCDE中,对角线AD、CE相交于F,求证:
如图,正五边形ABCDE中,对角线AD、CE相交于F,求证: 如图,PA,PB分别切圆O于点A,B,OP交AB于点M.若AB=6
如图,PA,PB分别切圆O于点A,B,OP交AB于点M.若AB=6 如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度.
如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度. 如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE.
如图,等边三角形ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边三角形CDE,连接BE. 如图1,四边形ABCD中,AD=CD,∠BAD=∠BCD.
如图1,四边形ABCD中,AD=CD,∠BAD=∠BCD.