题目内容
10.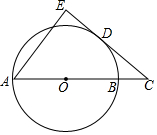 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA(1)求证:CD是⊙O的切线;
(2)AE⊥CD交CD的延长线于点E,若tanA=$\frac{\sqrt{7}}{3}$,AE=6,求⊙O的直径.
分析 (1)首先连接OD、DA、DB,由DC2=CB•CA,易证得△DCB∽△ACD,又由AB是⊙O的直径,继而可求得∠BDC+∠ODB=90°,则可证得结论;
(2)由tanA=$\frac{\sqrt{7}}{3}$,AE=6,可求得CE的长,继而求得AC的长,然后由OD∥AE,可得$\frac{OD}{AE}$=$\frac{OC}{AC}$,则可求得答案.
解答 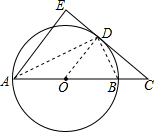 证明:(1)连接OD、DA、DB,
证明:(1)连接OD、DA、DB,
∵DC2=CB•CA,
∴$\frac{DC}{CA}$=$\frac{CB}{CD}$,
又∵∠DCB=∠ACD,
∴△DCB∽△ACD,
∴∠BDC=∠DAC,
∵OA=OD,
∴∠OAD=∠ODA,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠BDC+∠ODB=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)在Rt△ACE中,tanA=$\frac{CE}{AE}$=$\frac{CE}{6}$=$\frac{\sqrt{7}}{3}$,
∴CE=2$\sqrt{7}$,
在Rt△ACE中,AC=$\sqrt{{6}^{2}+(2\sqrt{7})^{2}}$=8,
∵OD∥AE,
∴$\frac{OD}{AE}$=$\frac{OC}{AC}$,
∴$\frac{r}{6}$=$\frac{8-r}{8}$,
解得:r=$\frac{24}{7}$,
∴⊙O的直径为$\frac{48}{7}$.
点评 此题考查了相似三角形的判定与性质、切线的判定、勾股定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.抛掷一枚质地均匀的骰子,两次都出现偶数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
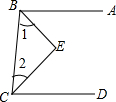 已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.
已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.
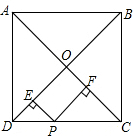 如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.
如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.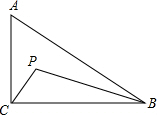 如图,Rt△ABC中,AC⊥BC,AC=8,BC=12,P是△ABC内部的一个动点,且满足∠PCA=∠PBC,则线段AP长的最小值为4.
如图,Rt△ABC中,AC⊥BC,AC=8,BC=12,P是△ABC内部的一个动点,且满足∠PCA=∠PBC,则线段AP长的最小值为4.