题目内容
1.某市推行高效课堂教学改革,已知小红所在的九(2)班有30人,恰好分成5个学习小组(记为A、B、C、D、E).(1)在李老师的一次随机点名中,求恰好点到小红的概率是多少;
(2)数学老师在某次课堂中设置了2个学习小组的展示成果,请用树形图或列表法求出随机恰好点到A、B学习小组展示成果的概率.
分析 (1)直接利用概率公式求出答案;
(2)利用树状图列举出所有可能,进而利用概率公式求出答案.
解答 解:(1)∵小红所在的九(2)班有30人,
∴在李老师的一次随机点名中,P(点到小红)=$\frac{1}{30}$;
(2)树状图如下:
可得,一共有20种可能,恰好点到A、B学习小组展示成果的有2种,
故P(点到A、B学习小组)=$\frac{2}{20}$=$\frac{1}{10}$.
点评 此题主要考查了树状图法求概率,正确利用树状图列举出所有可能是解题关键.

练习册系列答案
相关题目
11.下列各单项式中,与2xy是同类项的是( )
| A. | xy | B. | 3y | C. | 2x3y2 | D. | 4x |
12.用“*”定义一种运算:a*b=b3-ab,那么多项式4*a因式分解的结果是( )
| A. | a(a2+4) | B. | (a+4)(a-4) | C. | a(a+4)(a-4) | D. | a(a+2)(a-2) |
 如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P在边AB上运动,过点P作PQ⊥AB交折线AC-CB于点Q,Rt△EDF的斜边EF在射线BC上,DF∥AB,DF=AP,且DF与AB的距离为$\frac{AP}{2}$,设△EDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6)
如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P在边AB上运动,过点P作PQ⊥AB交折线AC-CB于点Q,Rt△EDF的斜边EF在射线BC上,DF∥AB,DF=AP,且DF与AB的距离为$\frac{AP}{2}$,设△EDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6) 推理填空
推理填空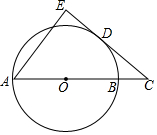 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA