题目内容
5.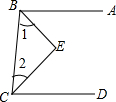 已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.
已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.证明:∵BE平分∠ABC.已知
∴∠ABC=2∠1.角平分线的定义
同理:∠BCD=2∠2.
∴∠ABC+∠BCD=2(∠1+∠2).等式的性质
∵∠1+∠2=90°.已知
∴∠ABC+∠BCD=2(∠1+∠2)=2×90°=180°.等量代换
∴AB∥CD.同旁内角互补,两直线平行.
分析 先根据角平分线的定义得出∠ABC=2∠1,∠BCD=2∠2,再由∠1+∠2=90°可得出∠ABC+∠BCD=180°,由此可得出结论.
解答 证明:∵BE平分∠ABD(已知),
∴∠ABC=2∠1(角平分线的定义).
∵CE平分∠DCB(已知),
∴∠BCD=2∠2(角平分线的定义),
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)(等式的性质)
又∵∠1+∠2=90°(已知)
∴∠ABC+∠BCD=2×90°=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:已知;∠ABC=2∠1;角平分线的定义;∠BCD=2∠2;等式的性质;∠1+∠2=90°;已知;∠ABC+∠BCD=2(∠1+∠2)=2×90°=180°;等量代换;同旁内角互补,两直线平行.
点评 本题考查的是平行线的判定,关键是利用同旁内角互补,两直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.多项式1+2xy-3xy2的次数是( )
| A. | 3 | B. | -3 | C. | 5 | D. | 6 |
9.下列运算中,错误的是( )
| A. | 3x4+5x4=8x4 | B. | -3x3+5x3=2x3 | C. | 4x6-8x6=-4 | D. | 4x6-8x6=-4x6 |
 推理填空
推理填空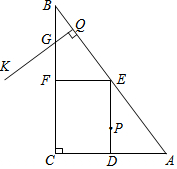 如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).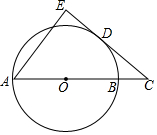 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA