题目内容
2.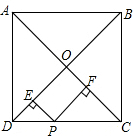 如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.
如图所示,在正方形ABCD中,若对角线的长为10cm,P是CD上任意一点,过点P分别作PE⊥BD,PF⊥AC,垂足分别为E,F,则PE+PF=5cm.
分析 连接OP,根据正方形的性质得出AC=BD=10cm,OB=OC=5cm,∠DOC=90°,根据三角形的面积得出S△DOP+S△COP=S△DOC,代入求出即可.
解答 解:连接OP,
∵四边形ABCD是正方形,
∴AC=BD=10cm,OB=OC=5cm,∠DOC=90°,
∴S△DOP+S△COP=S△DOC,
∴$\frac{1}{2}$×5×PE+$\frac{1}{2}$×5×PF=$\frac{1}{2}$×5×5,
∴PE+PF=5,
故答案为:5.
点评 本题考查了正方形的性质,三角形的面积的应用,熟记正方形的各种性质以及整体数学思想的运用是解题的关键.

练习册系列答案
相关题目
12.用“*”定义一种运算:a*b=b3-ab,那么多项式4*a因式分解的结果是( )
| A. | a(a2+4) | B. | (a+4)(a-4) | C. | a(a+4)(a-4) | D. | a(a+2)(a-2) |
6. 如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )
如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )
 如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )
如图,已知DE∥FG∥BC,且GA:AD:DB=3:4:2,则S△AGF:S△ADE:S△ABC的值是( )| A. | 3:4:2 | B. | 3:4:6 | C. | 9:16:20 | D. | 9:16:36 |
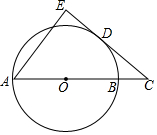 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA