题目内容
4.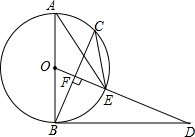 如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.
如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.(I)求证:∠ODB=∠AEC;
(2)若⊙O的半径为4,sinA=$\frac{3}{4}$,求EF的长.
分析 (1)根据已知条件得到∠ABD=90°,根据余角的性质得到∠ODB=∠OBF,等量代换即可得到结;
(2)连接BE,由AB是⊙O的直径,得到∠AEB=90°,等量代换得到∠EBF=∠A,根据三角函数的定义得到BE=6,于是得到结论.
解答 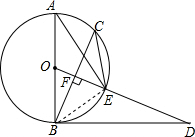 解:(1)∵AB是⊙O的直径,BD是⊙O的切线,
解:(1)∵AB是⊙O的直径,BD是⊙O的切线,
∴∠ABD=90°,
∵0D⊥BC,
∴∠OFB=90°,
∴∠OBF+∠BOF=∠BOF+∠D=90°,
∴∠ODB=∠OBF,
∵∠OBF=∠AEC,
∴∠ODB=∠AEC;
(2)连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠A+∠ABE=90°,
∵OB=OE,
∴∠ABE=∠OEB,
∵∠FBE+∠BEF=90°,
∴∠EBF=∠A,
∵⊙O的半径为4,
∴AB=8,
∵sinA=$\frac{3}{4}$,
∴BE=6,
∵sin∠EBF=sinA=$\frac{3}{4}$,
∴EF=$\frac{9}{2}$.
点评 本题考查了切线的性质,三角函数的定义,圆周角定理,连接BE构造直角三角形是解题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
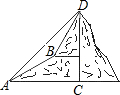 如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)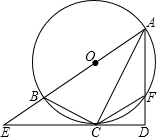 如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.
如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.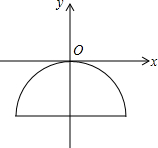 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米. 已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.
已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.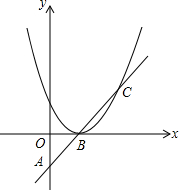 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC. 如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.
如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.