题目内容
14. 如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.
如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.
分析 作CH⊥x轴于H,如图,先计算出∠BAO=60°,再根据旋转的性质得到∠DAC=∠BAO=60°,AC=AO=1,在Rt△ACH中利用含30度的直角三角形三边的关系得到AH=$\frac{1}{2}$AC=$\frac{1}{2}$,CH=$\sqrt{3}$AH=$\frac{\sqrt{3}}{2}$,于是得到C点坐标,然后根据反比例函数图象上点的坐标特征可计算出k的值.
解答 解:作CH⊥x轴于H,如图,
在Rt△OAB中,∵∠OBA=30°,
∴∠BAO=60°,
∵△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,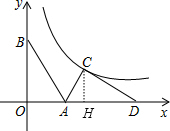
∴∠DAC=∠BAO=60°,AC=AO=1,
在Rt△ACH中,∵∠ACH=30°,
∴AH=$\frac{1}{2}$AC=$\frac{1}{2}$,CH=$\sqrt{3}$AH=$\frac{\sqrt{3}}{2}$,
∴C($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
∵点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=$\frac{3}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
故答案为$\frac{3\sqrt{3}}{4}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了旋转的性质.

练习册系列答案
相关题目
5.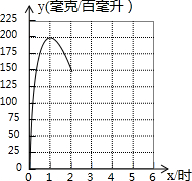 某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
(1)求出1.5小时内血液中含药量y1与时间x之间的函数关系式.
(2)在坐标系中描出上述表格中各点,猜想并求出1.5小时后血液中含药量y2与时间x所满足的函数关系式.
(3)当血液中的含药量大于或等于72毫克/百毫升时属于“治疗最佳期”,请问:服药后哪一段时间属于“治疗最佳期”?
(4)当血液中的含药量大于或等于30毫克/百毫升时属于“治疗有效期”,假设某病人晚上20:00服药,第二天早上7:00时是否应该再一次服药,请说明理由.
 某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:| x | 1.5 | 2.5 | 3 | 4.5 | 5 | … |
| y | 150 | 90 | 75 | 50 | 45 | … |
(2)在坐标系中描出上述表格中各点,猜想并求出1.5小时后血液中含药量y2与时间x所满足的函数关系式.
(3)当血液中的含药量大于或等于72毫克/百毫升时属于“治疗最佳期”,请问:服药后哪一段时间属于“治疗最佳期”?
(4)当血液中的含药量大于或等于30毫克/百毫升时属于“治疗有效期”,假设某病人晚上20:00服药,第二天早上7:00时是否应该再一次服药,请说明理由.
2.下列计算正确的是( )
| A. | -22=4 | B. | ${({-\frac{1}{2}})^{-2}}=4$ | C. | (-3)-1×3=1 | D. | (-1)2016=2016 |
9.已知:点A(x1,y1),B(x2,y2),C(x3,y3)是函数y=-$\frac{3}{x}$图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | 无法确定 |
19.画出函数y=-2x+1(x>0)的图象
(1)计算并填写表中的空格
(2)根据表中的数值在平面直角系中描点,坐标为(-2,5),(-1,3),(0,1),(1,-2),(2,3)
(3)用平滑的曲线连接这些点.
(1)计算并填写表中的空格
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | -1 | -3 | … |
(3)用平滑的曲线连接这些点.
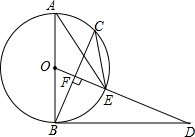 如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.
如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.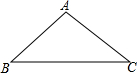 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC. 如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.
如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.