题目内容
19.已知α、β是方程x2+2x-5=0的两个实数根,则α2-β2的值为4$\sqrt{6}$或-4$\sqrt{6}$.分析 根据韦达定理求出α+β、αβ,再根据(α-β)2=(α+β)2-4αβ求出α-β的值,再代入计算即可.
解答 解:根据韦达定理有:α+β=-2 αβ=-5,
∵(α-β)2=(α+β)2-4αβ=4+20=24
∴α-β=±2$\sqrt{6}$,
∴α2-β2=(α+β)(α-β)=(-2)×(±2$\sqrt{6}$)=±4$\sqrt{6}$,
故答案为:4$\sqrt{6}$或-4$\sqrt{6}$.
点评 本题考查了一元二次方程的根与系数的关系,能将根与系数的关系与代数式变形相结合是解决问题的关键.

练习册系列答案
相关题目
14.已知⊙O的半径为4cm,直线l与⊙O相切,则圆心O与直线l的距离为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 无法确定 |
11.下列各组中的四条线段成比例的是( )
| A. | 6cm、2cm、1cm、4cm | B. | 4cm、5cm、6cm、7cm | C. | 3cm、4cm、5cm、6cm | D. | 6cm、3cm、8cm、4cm |
9.已知:点A(x1,y1),B(x2,y2),C(x3,y3)是函数y=-$\frac{3}{x}$图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | 无法确定 |
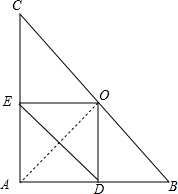 如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.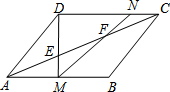 平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.
平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.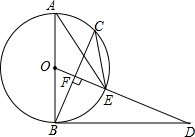 如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.
如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.