题目内容
9.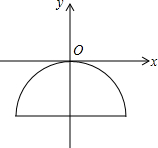 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.(1)求抛物线的关系式;
(2)求距离y轴5米的石拱桥的高度.
分析 (1)根据函数图象和题目中的信息,可以分别得到点A的坐标和点O的坐标,然后设出抛物线的解析式,即可求得抛物线的解析式;
(2)根据第一问求得的解析式,将x代入解析式可以求得相应的y的值,然后即可转化为距离y轴5米的石拱桥的高度.
解答 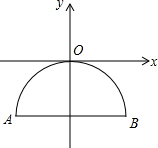 解:(1)如右图所示,
解:(1)如右图所示,
由题意可得,点A的坐标是(-23,-16),抛物线顶点O的坐标是(0,0),
设该抛物线的解析式是y=ax2,
则-16=a×(-23)2,
解得,a=$-\frac{16}{529}$,
即抛物线的关系式y=$-\frac{16}{529}{x}^{2}$;
(2)将x=-5代入y=$-\frac{16}{529}{x}^{2}$,得$y=-\frac{16}{529}×{(-5)}^{2}=-\frac{400}{529}$,
∴距离y轴5米的石拱桥的高度是:$(-\frac{400}{529})-(-16)$=$\frac{8064}{529}$米,
即距离y轴5米的石拱桥的高度是$\frac{8064}{529}$米.
点评 本题考查二次函数的应用,解题的关键是明确题意,利用数学中转化的数学思想和数形结合的数学思想解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列计算中正确的是( )
| A. | (x-1)-2=x2 | B. | x2n÷x2=xn(n是正整数) | ||
| C. | (-2x2)3=-6x6 | D. | (-3a-2)(3a-2)=9a2-4 |
19.画出函数y=-2x+1(x>0)的图象
(1)计算并填写表中的空格
(2)根据表中的数值在平面直角系中描点,坐标为(-2,5),(-1,3),(0,1),(1,-2),(2,3)
(3)用平滑的曲线连接这些点.
(1)计算并填写表中的空格
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | -1 | -3 | … |
(3)用平滑的曲线连接这些点.
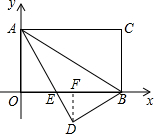 如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.
如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.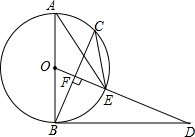 如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.
如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.