题目内容
16. 已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.
已知二次函数y=ax2+bx+c的图象如图所示,试确定a,b,c,2a+b,2a-b,a+b+c,a-b+c的符号.
分析 根据对称轴确定出a是负数,再根据对称轴大于0即可确定b>0,抛物线交于y轴的正半轴即可确定c>0,根据抛物线对称轴x=-$\frac{b}{2a}$<1,a<0,即可确定2a+b<0,根据a和b的符号,即可确定2a-b<0,由x=1,y>0,x=-1,y<0即可判定a+b+c>0,a-b+c<0.
解答 解:根据图象开口向下,a<0,
又∵对称轴直线x=-$\frac{b}{2a}$>0,
∴b>0,
抛物线交于y轴的正半轴,
∴c>0;
抛物线对称轴x=-$\frac{b}{2a}$<1,a<0,
∴-b>2a,
∴2a+b<0,
∵a<0,b>0,
∴2a-b<0,
根据图象,当x=1时,y>0,
∴a+b+c>0
根据图象,当x=-1时,y<0,
∴a-b+c<0.
点评 本题综合考查了二次函数图象与系数的关系,根据对称轴的情况,二次函数图象与x轴的交点的情况,以及特殊值进行解答,是基础题,难度不大.

练习册系列答案
相关题目
11.下列各组中的四条线段成比例的是( )
| A. | 6cm、2cm、1cm、4cm | B. | 4cm、5cm、6cm、7cm | C. | 3cm、4cm、5cm、6cm | D. | 6cm、3cm、8cm、4cm |
5.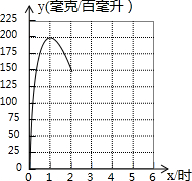 某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
(1)求出1.5小时内血液中含药量y1与时间x之间的函数关系式.
(2)在坐标系中描出上述表格中各点,猜想并求出1.5小时后血液中含药量y2与时间x所满足的函数关系式.
(3)当血液中的含药量大于或等于72毫克/百毫升时属于“治疗最佳期”,请问:服药后哪一段时间属于“治疗最佳期”?
(4)当血液中的含药量大于或等于30毫克/百毫升时属于“治疗有效期”,假设某病人晚上20:00服药,第二天早上7:00时是否应该再一次服药,请说明理由.
 某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:| x | 1.5 | 2.5 | 3 | 4.5 | 5 | … |
| y | 150 | 90 | 75 | 50 | 45 | … |
(2)在坐标系中描出上述表格中各点,猜想并求出1.5小时后血液中含药量y2与时间x所满足的函数关系式.
(3)当血液中的含药量大于或等于72毫克/百毫升时属于“治疗最佳期”,请问:服药后哪一段时间属于“治疗最佳期”?
(4)当血液中的含药量大于或等于30毫克/百毫升时属于“治疗有效期”,假设某病人晚上20:00服药,第二天早上7:00时是否应该再一次服药,请说明理由.
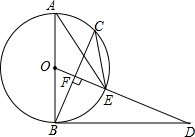 如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.
如图,AB是⊙O的直径,BD是⊙O的切线,点C为⊙O上一点,0D⊥BC于点F交⊙O于点E,连接AE、C′E.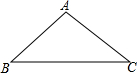 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.