题目内容
按下图方式摆放餐桌和椅子,
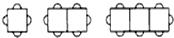
(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐 人.
(2)按照上图的方式继续排列餐桌,完成下表.
(3)一家餐厅有40张这样的长方形餐桌,某用餐单位要求餐厅按照上图方式每8张长方形餐桌拼成1张大桌子,则该餐厅此时能容纳多少人用餐?

(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐
(2)按照上图的方式继续排列餐桌,完成下表.
| 桌子张数 | 3 | 4 | 5 | n |
| 可坐人数 |
考点:规律型:图形的变化类
专题:
分析:(1)直接观察图形写出答案即可;
(2)桌子数每增加一张,人数增加2人,则依次填8、10、12、2n+4;每8张拼成1张大桌子,可坐2×8+4=20人,则9张大桌子可坐180人;
(3)代入n=8求得总人数,然后确定40张共摆成5大张求得总人数即可.
(2)桌子数每增加一张,人数增加2人,则依次填8、10、12、2n+4;每8张拼成1张大桌子,可坐2×8+4=20人,则9张大桌子可坐180人;
(3)代入n=8求得总人数,然后确定40张共摆成5大张求得总人数即可.
解答:解:(1)观察发现:2张长方形餐桌拼在一起可坐6人;
(2)填表如下:
(3)当n=8时,2n+2=2×8+2=18,
18×(40÷8)=90(人).
答:该餐厅此时能容纳90人用餐.
(2)填表如下:
| 桌子张数 | 3 | 4 | 5 | n |
| 可坐人数 | 8 | 10 | 12 | 2n+2 |
18×(40÷8)=90(人).
答:该餐厅此时能容纳90人用餐.
点评:考查了规律型:图形的变化类,本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解答此类题目一定要认真观察和分析数据,从中找出规律.

练习册系列答案
相关题目
已知二次函数y=3x2-6x+5,若它的顶点不动,把开口反向,再沿对称轴平移,得到一条新抛物线,它恰好与直线y=mx-2交于点(2,4),则新抛物线的解析式为( )
| A、y=3x2+6x-4 |
| B、y=3x2+6x+4 |
| C、y=3x2-6x+4 |
| D、y=6x2-3x+4 |
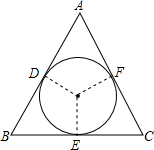 如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.