题目内容
已知二次函数y=3x2-6x+5，若它的顶点不动，把开口反向，再沿对称轴平移，得到一条新抛物线，它恰好与直线y=mx-2交于点（2，4），则新抛物线的解析式为（ ）
| A、y=3x2+6x-4 |
| B、y=3x2+6x+4 |
| C、y=3x2-6x+4 |
| D、y=6x2-3x+4 |
考点：二次函数图象与几何变换
专题：几何变换
分析：先把y=3x2-6x+5配成顶点式得到y=3（x-1）2+2，则顶点坐标为（1，2），由于新抛物线与原抛物线顶点一样，开口反向，且沿对称轴平移，则可设y=-3（x-1）2+2+t，然后把（2，4）代入求出t的值即可．
解答：解：y=3x2-6x+5=3（x-1）2+2，则抛物线的对称轴为直线x=1，顶点坐标为（1，2），
设新抛物线解析式为y=-3（x-1）2+2+t，
把（2，4）代入得-3•（2-1）2+2+t=4，解得t=5，
所以新抛物线解析式为y=-3（x-1）2+2+5=-3x2+6x+4．
故选B．
设新抛物线解析式为y=-3（x-1）2+2+t，
把（2，4）代入得-3•（2-1）2+2+t=4，解得t=5，
所以新抛物线解析式为y=-3（x-1）2+2+5=-3x2+6x+4．
故选B．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
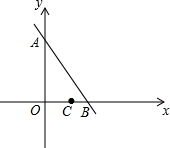如图，已知点A（0，6），B（3，0），C（2，0）．设点M的坐标为（0，m），其中m＜6，以M为圆心，MC为半径作圆．
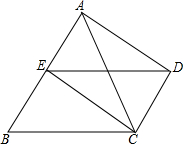已知，如图，△ABC中，E为AB的中点，DC∥AB，且DC=