题目内容
已知点A(3,4)、B(n,0)在一次函数y=2x+m的图象上.
(1)分别求m、n的值;
(2)能否在y轴上找一点P,使PA+PB的值最小?若能,请求出点P的坐标;若不能,请说明理由.
(3)在x轴上是否存在点Q,使得以点Q、O、A为顶点的三角形为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)分别求m、n的值;
(2)能否在y轴上找一点P,使PA+PB的值最小?若能,请求出点P的坐标;若不能,请说明理由.
(3)在x轴上是否存在点Q,使得以点Q、O、A为顶点的三角形为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)把A点坐标代入直线解析式可求得m,把B点坐标代入直线解析式可求得n;
(2)存在,可先求得B点关于y轴的对称点B′,连接B′A交y轴于一点P,则该点即为所可,根据A、B′的坐标可求得直线AB′的解析式,可求得P点坐标;
(3)分OA=OQ、OA=AQ和OQ=AQ三种情况,分别根据条件得到关于Q点的坐标的方程,可求得Q点的坐标.
(2)存在,可先求得B点关于y轴的对称点B′,连接B′A交y轴于一点P,则该点即为所可,根据A、B′的坐标可求得直线AB′的解析式,可求得P点坐标;
(3)分OA=OQ、OA=AQ和OQ=AQ三种情况,分别根据条件得到关于Q点的坐标的方程,可求得Q点的坐标.
解答:解:(1)∵A点在一次函数图象上,
∴6+m=4,解得m=-2,
∴直线解析式为y=2x-2,
又∵B点在一次函数图象上,
∴2n-2=0,
解得n=1;
(2)由(1)可知B点坐标为(1,0),则其关于y轴的对称点B′为(-1,0),
如图1,连接AB′交y轴于点P,则PA+PB的值最小,
设直线AB′解析式为y=kx+b,
把A、B′两点坐标代入可得
,
解得
,
∴直线AB′的解析式为y=x+1,
∴P点坐标为(0,1),
即在y轴上存在P点使PA+PB的值最小,其坐标为(0,1);

(3)由A(3,4)可求得OA=5,
当△OAQ为等腰三角形时,分三种情况:
①当OA=OQ时,则OQ=5,设Q点的坐标为(x,0),则有|x|=5,解得x=5或-5,所以Q点的坐标为(5,0)或(-5,0);
②当OA=AQ时,过A作AM⊥x轴于点M,如图2,
则OM=MQ=4,所以OQ=2OM=8,则Q点的坐标为(8,0);
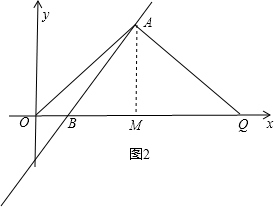
③当OQ=AQ时,设Q坐标为(x,0),过A作AN⊥x轴于点N,如图3,

则OQ=AQ=x,NQ=ON-OQ=|3-x|,且AN=4,
在Rt△ANQ中,由勾股定理可得AQ2=AN2+NQ2,
即x2=42+(3-x)2,解得x=
,则Q点的坐标为(
,0);
综上可知在x轴上存在点Q使△OAQ为等腰三角形,Q点的坐标为(5,0)或(-5,0)或(8,0)或(
,0).
∴6+m=4,解得m=-2,
∴直线解析式为y=2x-2,
又∵B点在一次函数图象上,
∴2n-2=0,
解得n=1;
(2)由(1)可知B点坐标为(1,0),则其关于y轴的对称点B′为(-1,0),
如图1,连接AB′交y轴于点P,则PA+PB的值最小,
设直线AB′解析式为y=kx+b,
把A、B′两点坐标代入可得
|
解得
|
∴直线AB′的解析式为y=x+1,
∴P点坐标为(0,1),
即在y轴上存在P点使PA+PB的值最小,其坐标为(0,1);

(3)由A(3,4)可求得OA=5,
当△OAQ为等腰三角形时,分三种情况:
①当OA=OQ时,则OQ=5,设Q点的坐标为(x,0),则有|x|=5,解得x=5或-5,所以Q点的坐标为(5,0)或(-5,0);
②当OA=AQ时,过A作AM⊥x轴于点M,如图2,
则OM=MQ=4,所以OQ=2OM=8,则Q点的坐标为(8,0);

③当OQ=AQ时,设Q坐标为(x,0),过A作AN⊥x轴于点N,如图3,

则OQ=AQ=x,NQ=ON-OQ=|3-x|,且AN=4,
在Rt△ANQ中,由勾股定理可得AQ2=AN2+NQ2,
即x2=42+(3-x)2,解得x=
| 25 |
| 6 |
| 25 |
| 6 |
综上可知在x轴上存在点Q使△OAQ为等腰三角形,Q点的坐标为(5,0)或(-5,0)或(8,0)或(
| 25 |
| 6 |
点评:本题主要考查待定系数法求函数解析式及轴对称的性质、等腰三角形的性质等知识的综合应用,在(1)中掌握点的坐标满足函数的解析式是解题关键,在(2)中确定出P点的位置是解题的关键,在(3)中分三种情况分别得出关于Q点的坐标的方程是解题的关键,注意分类讨论思想的应用,难度不大,属于基础知识的综合.

练习册系列答案
相关题目
 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
 甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:
甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示: