题目内容
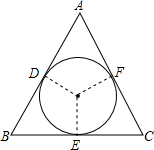 如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.考点:三角形的内切圆与内心
专题:计算题
分析:连结OD、OE、OF,设⊙O的半径为r,先根据等腰直角三角形的性质得BC=
AB=2
,再根据切线的性质得OD⊥AB,OF⊥AC,接着证明四边形ADOF为正方形,得到AD=AF=OD=r,则BD=2-r,CF=2-r,然后根据切线长定理得BE=BD=2-r,CE=CF=2-r,所以2-r+2-r=2
,再解方程即可.
| 2 |
| 2 |
| 2 |
解答:解: 连结OD、OE、OF,设⊙O的半径为r,
连结OD、OE、OF,设⊙O的半径为r,
在Rt△ABC中,∵∠CAB=90°,AB=AC=2,
∴BC=
AB=2
,
∵⊙O与AB,CA分别相切于点D、F,
∴OD⊥AB,OF⊥AC,
∵∠A=90°,
∴四边形ADOF为矩形,
∵OD=OF,
∴四边形ADOF为正方形,
∴AD=AF=OD=r,
∴BD=2-r,CF=2-r,
∵⊙O与BC相切于点E,
∴BE=BD=2-r,CE=CF=2-r,
∴2-r+2-r=2
,
∴r=2-
,
即⊙O的半径为2-
.
 连结OD、OE、OF,设⊙O的半径为r,
连结OD、OE、OF,设⊙O的半径为r,在Rt△ABC中,∵∠CAB=90°,AB=AC=2,
∴BC=
| 2 |
| 2 |
∵⊙O与AB,CA分别相切于点D、F,
∴OD⊥AB,OF⊥AC,
∵∠A=90°,
∴四边形ADOF为矩形,
∵OD=OF,
∴四边形ADOF为正方形,
∴AD=AF=OD=r,
∴BD=2-r,CF=2-r,
∵⊙O与BC相切于点E,
∴BE=BD=2-r,CE=CF=2-r,
∴2-r+2-r=2
| 2 |
∴r=2-
| 2 |
即⊙O的半径为2-
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:
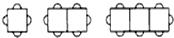
甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示: 如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.
如图,正六边形ABCDEF内接于⊙O,P为弧BC上一点,试判断PC,PA,PB之间的数量关系,并证明.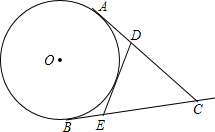 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系. 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.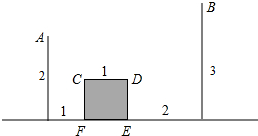 如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于
如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于