题目内容
在△ABC中，已知三边a、b、c满足a4+2a2b2+b4-2a3b-2ab3=0．试判断△ABC的形状．并证明你的结论．
考点：因式分解的应用
专题：
分析：将原式利用完全平方公式分解因式，进而得出a=b，即可得出答案．
解答：解：△ABC是等腰三角形．
理由：a4+2a2b2+b4-2a3b-2ab3=0
（a2+b2）2-2ab（a2+b2）=0，
（a2+b2）（a2+b2-2ab）=0，
故（a2+b2）（a-b）2=0，
则a=b，
故△ABC是等腰三角形．
理由：a4+2a2b2+b4-2a3b-2ab3=0
（a2+b2）2-2ab（a2+b2）=0，
（a2+b2）（a2+b2-2ab）=0，
故（a2+b2）（a-b）2=0，
则a=b，
故△ABC是等腰三角形．
点评：此题主要考查了因式分解的应用，正确分解因式是解题关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
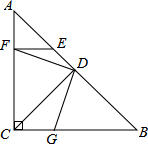已知在△ABC中，∠ACB=90°，AC=BC，CD⊥AB，垂足为D，E是AB上一点，EF⊥AC，垂足为F，G是BC上一点，CG=EF，求证：DF=DG．
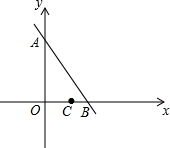如图，已知点A（0，6），B（3，0），C（2，0）．设点M的坐标为（0，m），其中m＜6，以M为圆心，MC为半径作圆．