题目内容
若a,b是△ABC的两边且|a-3|+b2-8b+16=0.
(1)试求a,b的值;并求第三边c的取值范围;
(2)若△ABC是等腰三角形,试求此三角形的周长;
(3)若另一等腰三角形△DEF,其中一个内角为x°,另一个内角为(2x-20)°,试求此三角形的各内角度数.
(1)试求a,b的值;并求第三边c的取值范围;
(2)若△ABC是等腰三角形,试求此三角形的周长;
(3)若另一等腰三角形△DEF,其中一个内角为x°,另一个内角为(2x-20)°,试求此三角形的各内角度数.
考点:等腰三角形的性质,非负数的性质:绝对值,非负数的性质:偶次方,三角形三边关系,三角形内角和定理
专题:
分析:(1)利用非负数的性质可求得a、b的值,根据三角形三边关系可求得c的范围;
(2)分腰长为3或4两种情况进行计算;
(3)分这两个内角一个为顶角和两个都是底角三种情况,结合三角形内角和定理可求得x,可得出三个角的度数.
(2)分腰长为3或4两种情况进行计算;
(3)分这两个内角一个为顶角和两个都是底角三种情况,结合三角形内角和定理可求得x,可得出三个角的度数.
解答:解:
(1)∵|a-3|+b2-8b+16=|a-3|+(b-4)2=0,
∴a=3 b=4,
∵b-a<c<b+a,
∴1<c<7;
(2)当腰长为3时,此时三角形的三边为3、3、4,满足三角形三边关系,周长为10;
当腰长为4时,此时三角形的三边长为4、4、3,满足三角形三边关系,周长为11;
综上可知等腰三角形的周长为10或11;
(3)当底角为x°、顶角为(2x-20)°时,则根据三角形内角和为180°可得
x+x+2x-20=180,
解得x=50,
此时三个内角分别为50°、50°、80°;
当顶角为x°、底角为(2x-20)°时,则根据三角形内角和为180°可得
x+2x-20+2x-20=180,
解得x=44,
此时三个内角分别为44°、68°、68°;
当底角为x°、(2x-20)°时,则等腰三角形性质可得
x=2x-20,
解得x=20,
此时三个内角分别为20°、20°、140°;
综上可知三角形三个内角为50度、50度、80度或44度、68度、68度或20度、20度、140度.
(1)∵|a-3|+b2-8b+16=|a-3|+(b-4)2=0,
∴a=3 b=4,
∵b-a<c<b+a,
∴1<c<7;
(2)当腰长为3时,此时三角形的三边为3、3、4,满足三角形三边关系,周长为10;
当腰长为4时,此时三角形的三边长为4、4、3,满足三角形三边关系,周长为11;
综上可知等腰三角形的周长为10或11;
(3)当底角为x°、顶角为(2x-20)°时,则根据三角形内角和为180°可得
x+x+2x-20=180,
解得x=50,
此时三个内角分别为50°、50°、80°;
当顶角为x°、底角为(2x-20)°时,则根据三角形内角和为180°可得
x+2x-20+2x-20=180,
解得x=44,
此时三个内角分别为44°、68°、68°;
当底角为x°、(2x-20)°时,则等腰三角形性质可得
x=2x-20,
解得x=20,
此时三个内角分别为20°、20°、140°;
综上可知三角形三个内角为50度、50度、80度或44度、68度、68度或20度、20度、140度.
点评:本题主要考查等腰三角形的性质,掌握等腰三角形的两腰相等、两底角相等是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
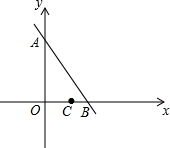 如图,已知点A(0,6),B(3,0),C(2,0).设点M的坐标为(0,m),其中m<6,以M为圆心,MC为半径作圆.
如图,已知点A(0,6),B(3,0),C(2,0).设点M的坐标为(0,m),其中m<6,以M为圆心,MC为半径作圆.
 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.