题目内容
3. 某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.
某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.(1)填空:a=80,b=8;
(2)请求出:当x>10时,y与x之间的函数关系式;
(3)导游小王带A旅游团到该景区旅游,付门票费用2720元(导游不需购买门票),求A旅游团有多少人?
分析 (1)根据函数图象可以求得a、b的值;
(2)根据函数图象可以求得当x>10时,y与x之间的函数关系式;
(3)根据(2)中的解析式可以求得A旅游团的人数.
解答 解:(1)由图象可知,
a=800÷10=80,
b=$\frac{1440-800}{10×80}×10$=8,
故答案为:80,8;
(2)当x>10时,设y与x之间的函数关系式是y=kx+m,
则$\left\{\begin{array}{l}{10k+m=800}\\{20k+m=1440}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=64}\\{m=160}\end{array}\right.$,
即当x>10时,y与x之间的函数关系式是y=64x+160;
(3)∵2720>800,
∴将y=2720代入y=64x+160,得
2720=64x+160,
解得,x=40,
即A旅游团有40人.
点评 本题考查一次函数的应用,揭帖关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.若3x2a+by2与-4x3y3a-b是同类项,则a-b的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.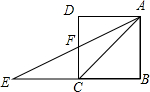 如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( )
如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( )
 如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( )
如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( )| A. | 22.5° | B. | 30° | C. | 45° | D. | 67.5° |
13.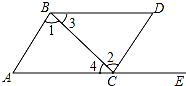 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠D=∠A | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠D=∠DCE |
 在正方形ABCD中,点E、F分别在AB、AD边上,△ADE绕着点O顺时针旋转到△DCF的位置,则旋转的角度是90(度).
在正方形ABCD中,点E、F分别在AB、AD边上,△ADE绕着点O顺时针旋转到△DCF的位置,则旋转的角度是90(度). 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F, 如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8.
如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8.