如图.点E在AC的延长线上.下列条件中能判断AB∥CD的是( )A．∠D=∠AB．∠1=∠2C．∠3=∠4D．∠D=∠DCE 题目和参考答案——青夏教育精英家教网—

题目内容

13．

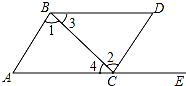如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

A．

∠D=∠A

B．

∠1=∠2

C．

∠3=∠4

D．

∠D=∠DCE

分析根据内错角相等，两直线平行可分析出∠1=∠2可判定AB∥CD．

解答解：A、∠D=∠A不能判定AB∥CD，故此选项不合题意；
B、∠1=∠2可判定AB∥CD，故此选项符合题意；
C、∠3=∠4可判定AC∥BD，故此选项不符合题意；
D、∠D=∠DCE判定直线AC∥BD，故此选项不合题意；
故选：B．

点评此题主要考查了平行线的判定，关键是掌握同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．

练习册系列答案

相关题目

3．

某旅游风景区门票价格为a元/人，对团体票规定：10人以下（包括10人）不打折，10人以上超过10人的部分打b 折，设游客为x人，门票费用为y元，y与x之间的函数关系如图所示．
（1）填空：a=80，b=8；
（2）请求出：当x＞10时，y与x之间的函数关系式；
（3）导游小王带A旅游团到该景区旅游，付门票费用2720元（导游不需购买门票），求A旅游团有多少人？

4．解方程组：
（1）$\left\{\begin{array}{l}x-y=-2\\ x+2y=4\end{array}\right.$
（2）$\left\{\begin{array}{l}\frac{x}{2}-\frac{y+1}{3}=1\\ 3x+2y=10\end{array}\right.$．

1．分解因式：
（1）4x²-16y²；
（2）a²b+4ab+4b．

8．方程x+2y=5的正整数解为x=3，y=1或x=1，y=2．

18．

如图，在矩形纸片ABCD中，CD=12，BC=15，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A₁处，求AE的长度．

7．

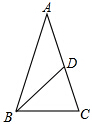如图，在△ABC中，AB=AC，∠A=36°，BD分别是△ABC的角平分线，则图中的等腰三角形共有（　　）

4．

如图是变量y与x之间的函数图象，则函数y的取值范围是（　　）

5．已知在Rt△ABC中，∠C=90°，AC=2，BC=3，则AB的长为（　　）

试题分类