题目内容
15. 如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8.
如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8.
分析 根据平移的性质,经过平移,对应点所连的线段平行且相等,可得四边形ABED是平行四边形,再根据平行四边形的面积公式即可求解.
解答 解:∵将△ABC沿CB向右平移得到△DEF,平移距离为2,
∴AD∥BE,AD=BE=2,
∴四边形ABED是平行四边形,
∴四边形ABED的面积=BE×AC=2×4=8.
故答案为:8.
点评 本题主要考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目
5. 如图,△ABC以O为旋转中心,旋转180°后得到△A′B′C′,ED是△ABC的中位线,经旋转后为线段 E′D′.已知BC=4,则E′D′等于( )
如图,△ABC以O为旋转中心,旋转180°后得到△A′B′C′,ED是△ABC的中位线,经旋转后为线段 E′D′.已知BC=4,则E′D′等于( )
 如图,△ABC以O为旋转中心,旋转180°后得到△A′B′C′,ED是△ABC的中位线,经旋转后为线段 E′D′.已知BC=4,则E′D′等于( )
如图,△ABC以O为旋转中心,旋转180°后得到△A′B′C′,ED是△ABC的中位线,经旋转后为线段 E′D′.已知BC=4,则E′D′等于( )| A. | 4 | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
6.下列方程中是一元一次方程的是( )
| A. | 4x-5=0 | B. | 3x-2y=3 | C. | 3x2-14=2 | D. | $\frac{1}{x}-2=3$ |
7.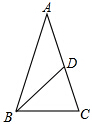 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.
某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.