Question

12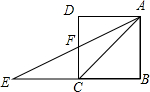．如图，E是正方形ABCD的边BC的延长线上一点，若CE=CA，AE交CD于F，则∠FAC的度数是（　　）

• A． 22.5°
• B． 30°
• C． 45°
• D． 67.5°

Answer 1

分析 由四边形ABCD是正方形，∠ACB=45°，然后由CE=CA，可得∠E=∠FAC，继而由三角形外角的性质，求得答案．

解答 解：∵四边形ABCD是正方形，
∴∠ACB=45°，
∴∠E+∠∠FAC=∠ACB=45°，
∵CE=CA，
∴∠E=∠FAC，
∴∠FAC=$\frac{1}{2}$∠ACB=22.5°．
故选A．

点评 此题考查了正方形的性质以及等腰三角形的性质．注意证得∠E=∠DAC=$\frac{1}{2}$∠ACB是解此题的关键．