题目内容
18.解下列不等式或不等式组,并将其解集在数轴上表示出来:(1)2(x+4)≥3(x-2)
(2)$\left\{\begin{array}{l}{x-3(x-2)<8}\\{\frac{2x+1}{5}>\frac{x-1}{2}}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)去括号,得:2x+8≥3x-6,
移项,得:2x-3x≥-6-8,
合并同类项,得:-x≥-14,
系数化为1,得:x≤14,
将解集表示在数轴上如下:
(2)解不等式x-3(x-2)<8,得:x>-1,
解不等式$\frac{2x+1}{5}$>$\frac{x-1}{2}$,得:x<7,
∴不等式组的解集为-1<x<7,
将不等式组的解集表示在数轴上如图:
点评 本题考查的是解一元一次不等式与不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
6.下列方程中是一元一次方程的是( )
| A. | 4x-5=0 | B. | 3x-2y=3 | C. | 3x2-14=2 | D. | $\frac{1}{x}-2=3$ |
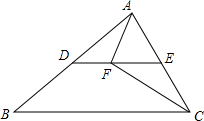 如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=2cm.
如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=2cm. 某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.
某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上 超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.