题目内容
9. 如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF.
如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF.
分析 过点B作BN∥AC交EM的延长线于N,根据两直线平行,内错角相等可得∠MBN=∠C,∠N=∠MFC,根据线段中点的定义可得BM=CM,然后利用“角角边”证明△BMN和△CMF全等,根据全等三角形对应边相等可得BN=CF,根据角平分线的定义求出∠BAD=∠CAD,然后根据平行线的性质求出∠E=∠BAD,∠N=∠CFM=∠CAD,从而得到∠E=∠N,再根据等角对等边可得BE=BN,最后等量代换即可得证.
解答  证明:如图,过点B作BN∥AC交EM的延长线于N,
证明:如图,过点B作BN∥AC交EM的延长线于N,
所以,∠MBN=∠C,∠N=∠MFC,
∵M为BC的中点,
∴BM=CM,
在△BMN和△CMF中,$\left\{\begin{array}{l}{∠MBN=∠C}\\{∠N=∠MFC}\\{BM=CM}\end{array}\right.$,
∴△BMN≌△CMF(AAS),
∴BN=CF,
∵AD为△ABC的角平分线,
∴∠BAD=∠CAD,
∵ME∥AD,
∴∠E=∠BAD,∠CFM=∠CAD,
∵BN∥AC,
∴∠N=∠CFM,
∴∠N=∠CFM=∠CAD,
∴∠E=∠N,
∴BE=BN,
∴BE=CF.
点评 本题考查了全等三角形的判定与性质,平行线的性质,角平分线的定义,等角对等边的性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于作辅助线构造出全等三角形并找出一条与BE、CF都相等的线段作为过渡桥梁.

练习册系列答案
相关题目
4. 春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.
春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.
(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:
观察表中数据,写出y随x变化的一个特征:y随x的增大先增大后减小.
 春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.
春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2.(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:
| x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
| y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
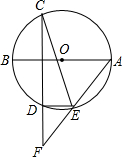 已知:如图,在⊙O中,直径AB垂直于弦CD,在CD的延长线上任取一点F,连AF交圆于E,连接DE,CE.求证:
已知:如图,在⊙O中,直径AB垂直于弦CD,在CD的延长线上任取一点F,连AF交圆于E,连接DE,CE.求证:
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒钟后△DPQ的面积等于28cm2?
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒钟后△DPQ的面积等于28cm2?