题目内容
14.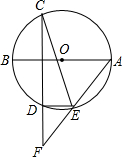 已知:如图,在⊙O中,直径AB垂直于弦CD,在CD的延长线上任取一点F,连AF交圆于E,连接DE,CE.求证:
已知:如图,在⊙O中,直径AB垂直于弦CD,在CD的延长线上任取一点F,连AF交圆于E,连接DE,CE.求证:(1)AC=AD;
(2)∠AEC=∠DEF.
分析 (1)连接AC与AD,利用垂径定理及圆的性质只需证明AC=AD即可(2)由(1)可知∠AEC=∠ACD、∠ADC=∠ACD,根据圆内接四边形的性质可知∠DEF=∠ACD
再根据等量代换即可得到证明.
解答 证明:(1)连接AC,
∵线段AB与线段CD分别是⊙O的直径和弦,且AB⊥CD,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠AEC=∠ACD,
∵$\widehat{AC}=\widehat{AC}$
∴∠ADC=∠AEC(同弧所对的圆周角相等)
∴∠ADC=∠ACD
∴AC=AD(等角对等边)
(2)∵四边形ACDE内接于⊙O,
∴∠DEF=∠ACD(圆内接四边形的一个外角等于它的内对角)
又由(1)可知∠ADC=∠ACD
∴∠ADC=∠DEF
又∵∠ADC=∠AEC(同弧所对的圆周角相等)
∴∠AEC=∠DEF
点评 本题考查了垂径定理、圆内接四边形的性质等知识点,解题的关键是掌握垂径定理、圆内接四边形的性质意义.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
19.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是h;因变量是t;
当地面上(即h=0时)时,温度是20℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
| 距离地面高度(千米)h | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃)t | 20 | 14 | 8 | 2 | -4 | -10 |
(1)表中自变量是h;因变量是t;
当地面上(即h=0时)时,温度是20℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
3.微山湖自古就有“日出斗金”之美誉,助推着周边地区经济的发展,某公司加工生产了A、B、C三类湖产品,销售的重量及利润如表所示:
该公司计划用26辆汽车装载三类湖产品(毎类湖产品至少一辆车,每辆汽车只装一类湖产品且装满)共48吨到某地销售.
(1)设装A类湖产品用x辆汽车,装B类湖产品用y辆汽车,装C类湖产品用z辆汽车.请用含z的式子表示x,y.
(2)如果本次销售公司获得利润为w万元,那么如何安排装运,可使w最大,最大是多少万元?
| 湖产品种类 | A类 | B类 | C类 |
| 每辆汽车装载吨数 | 2 | 1 | 1.5 |
| 每吨湖产品可获利润(万元) | 5 | 7 | 4 |
(1)设装A类湖产品用x辆汽车,装B类湖产品用y辆汽车,装C类湖产品用z辆汽车.请用含z的式子表示x,y.
(2)如果本次销售公司获得利润为w万元,那么如何安排装运,可使w最大,最大是多少万元?
 如图,边长为1的菱形ABCD中,∠DAB=60°,以对角线AC为边作第2个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第3个菱形AEGH使∠HAE=60°…,则第3个菱形的边长是3,按此规律所作第n个菱形的边长是($\sqrt{3}$)n-1.
如图,边长为1的菱形ABCD中,∠DAB=60°,以对角线AC为边作第2个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第3个菱形AEGH使∠HAE=60°…,则第3个菱形的边长是3,按此规律所作第n个菱形的边长是($\sqrt{3}$)n-1. 如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF.
如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF.
 如图,l1∥l2∥l3,且l1和l2间的距离是5,l2和l3间的距离是7,若正方形有三个顶点分别在三条直线上,则此正方形的面积最小是74.
如图,l1∥l2∥l3,且l1和l2间的距离是5,l2和l3间的距离是7,若正方形有三个顶点分别在三条直线上,则此正方形的面积最小是74.