题目内容
19. 如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.
如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.
分析 直接利用翻折变换的性质,结合矩形的性质得出∠CBN=∠2=∠3,进而得出∠BOC=90°,求出答案即可.
解答 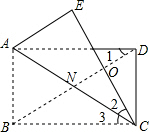 解:∵将长方形纸片ABCD沿AC翻折,点B落在点E处,
解:∵将长方形纸片ABCD沿AC翻折,点B落在点E处,
∴∠2=∠3,∠ABC=∠E=90°,
∵四边形ABCD是矩形,
∴BN=NC,
∴∠3=∠CBN,
∴∠CBN=∠2=∠3,
∵AE∥BD,
∴∠BOC=90°,
∴∠CBN=∠2=∠3=30°,
∴∠EAC的度数为60°.
故答案为:60.
点评 此题主要考查了平行线的性质以及矩形的性质和翻折变换,根据题意得出∠CBN=∠2=∠3是解题关键.

练习册系列答案
相关题目
14.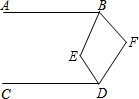 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )| A. | ∠E=∠F | B. | ∠E+∠F=180° | C. | 3∠E+∠F=360° | D. | 2∠E-∠F=90° |
8.若(m-1)2与$\sqrt{n+2}$互为相反数,则P(-m,-n)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
9.下列说法正确的是( )
| A. | 有且只有一条直线与已知直线平行 | |
| B. | 平行于同一条直线的两条直线互相垂直 | |
| C. | 从直线外一点与直线上各点连接的所有线中,垂线最短 | |
| D. | 在平面内过一点有且只有一条直线与已知直线垂直 |
 如图,反比例函数y=$\frac{k}{x}$图象上有一点P,PA⊥x轴于点A,点B在y轴的负半轴上,若△PAB的面积为4,则k=-8.
如图,反比例函数y=$\frac{k}{x}$图象上有一点P,PA⊥x轴于点A,点B在y轴的负半轴上,若△PAB的面积为4,则k=-8.