题目内容
9. 如图,反比例函数y=$\frac{k}{x}$图象上有一点P,PA⊥x轴于点A,点B在y轴的负半轴上,若△PAB的面积为4,则k=-8.
如图,反比例函数y=$\frac{k}{x}$图象上有一点P,PA⊥x轴于点A,点B在y轴的负半轴上,若△PAB的面积为4,则k=-8.
分析 由三角形的面积公式结合反比例函数系数k的几何意义即可得出关于k的含绝对值的一元一次方程,解方程可得出k的值,再由函数图象在第二、四象限即可得出结论.
解答 解:∵S△PAB=$\frac{1}{2}$PA•OA=$\frac{1}{2}$|k|=4,
∴k=±8,
∵反比例函数y=$\frac{k}{x}$的图象在第二、四象限,
∴k=-8.
故答案为:-8.
点评 本题考查了三角形的面积公式以及反比例函数系数k的几何意义,解题的关键是找出关于k的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,用三角形的面积公式表示出来三角形的面积,再结合反比例函数系数k的几何意义得出关于k的方程是关键.

练习册系列答案
相关题目
20.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{18a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{{x}^{3}y}$ | D. | $\sqrt{\frac{12}{5}}$ |
4.下列说法正确的是( )
| A. | 求sin30°的按键顺序是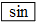 、30、= 、30、= | |
| B. | 求23的按键顺序 、2、 、2、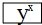 、3、= 、3、= | |
| C. | 求$\sqrt{8}$的按键顺序是 、 、 、8、= 、8、= | |
| D. | 已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是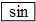 、 、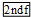 、0.5018、= 、0.5018、= |
14.下列计算正确的是( )
| A. | 3a+4b=7ab | B. | -a-1÷a=$\frac{1}{{a}^{2}}$ | C. | (2ab3)2=4a2b6 | D. | (x-y)2=x2-y2 |
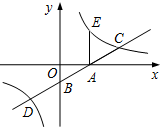 如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E. 如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.
如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.