题目内容
14.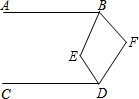 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )| A. | ∠E=∠F | B. | ∠E+∠F=180° | C. | 3∠E+∠F=360° | D. | 2∠E-∠F=90° |
分析 直接利用平行线的性质得出∠ABE+∠CDE=∠BED,进而利用四边形内角和定理得出2∠BED+∠BED+∠F=360°,即可得出答案.
解答 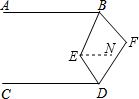 解:过点E作EN∥DC,
解:过点E作EN∥DC,
∵AB∥CD,
∴AB∥EN∥DC,
∴∠ABE=∠BEN,∠CDE=∠NED,
∴∠ABE+∠CDE=∠BED,
∵∠EBF=2∠ABE,∠EDF=2∠CDE,
∴设∠ABE=x,则∠EBF=2x,设∠CDE=y,则∠EDF=2y,
∵2x+2y+∠BED+∠F=360°,
∴2∠BED+∠BED+∠F=360°,
∴3∠BED+∠F=360°.
故选:C.
点评 此题主要考查了平行线的性质以及四边形内角和定理,正确得出∠ABE+∠CDE=∠BED是解题关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
4.下列说法正确的是( )
| A. | 求sin30°的按键顺序是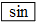 、30、= 、30、= | |
| B. | 求23的按键顺序 、2、 、2、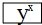 、3、= 、3、= | |
| C. | 求$\sqrt{8}$的按键顺序是 、 、 、8、= 、8、= | |
| D. | 已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是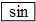 、 、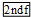 、0.5018、= 、0.5018、= |
2.下列四组线段中,能组成直角三角形的是( )
| A. | a=1,b=2,c=3 | B. | a=4,b=2,c=3 | C. | a=4,b=2,c=5 | D. | a=4,b=5,c=3 |
6. 如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )
如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )
 如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )
如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )| A. | 125° | B. | 130° | C. | 140° | D. | 155° |
3.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.添加的条件不能是( )
| A. | AB∥DC | B. | ∠A=90° | C. | ∠B=90° | D. | AC=BD |
4.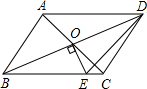 如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为6cm,则平行四边形ABCD的周长为( )
如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为6cm,则平行四边形ABCD的周长为( )
 如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为6cm,则平行四边形ABCD的周长为( )
如图,平行四边形ABCD的对角线相交于点O,且DC≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为6cm,则平行四边形ABCD的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
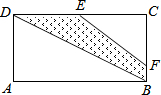 如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF=$\frac{1}{4}$BC,则四边形DBFE的面积为( )
如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF=$\frac{1}{4}$BC,则四边形DBFE的面积为( ) 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,图中四条线段的端点均在格点上.
如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,图中四条线段的端点均在格点上. 如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.
如图,将长方形纸片ABCD沿AC翻折,点B落在点E处,连接BD,若∠ADB=∠ACB,AE∥BD,则∠EAC的度数为60°.