题目内容
4．
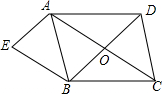如图，在?ABCD中，对角线AC、BD相交于点O，AE∥BD，BE∥AC，AE与BE相交于点E，当AB，AD满足什么条件时，四边形AEBO为矩形？请说明埋由．
分析 先证明四边形AEBO是平行四边形，再证明四边形ABCD是菱形，得出AC⊥BD，因此∠AOB=90°，即可得出四边形AEBO是矩形．
解答 解：AB=AD时，四边形AEBO为矩形；理由如下：
∵AE∥BD，BE∥AC，
∴四边形AEBO是平行四边形，
∵AB=AD，
∴四边形ABCD是菱形，
∴AC⊥BD，
∴∠AOB=90°，
∴四边形AEBO是矩形．
点评 本题考查了平行四边形的判定，矩形的判定，菱形的判定与性质等知识点的应用，注意：有一个角是直角的平行四边形是矩形．
练习册系列答案
相关题目
如图，AC∥CD，AP和CP分别平分∠BAC和∠ACD，过点P分别作PG⊥AC于点G，PE⊥AB于点E，EP的延长线交CD于点F．
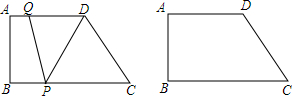
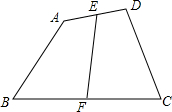四边形ABCD中，E，F分别为AD，BC的中点，EF=m，则AB+CD的最小值为2m．
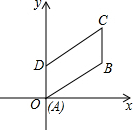如图，在平行四边形ABCD中，∠DAB=60°，AB=2，AD=1，若点A在坐标原点，AB与x轴的夹角为30°，求平行四边形各顶点的坐标．
如图，?ABED中，对角线BD平分∠ABE，过点D作DC∥AE，交BE的延长线于点C．求证：AB=CE．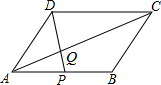
如图，在?ABCD中，点P在AB上，连结DP，交AC于点Q，当点P是AB的中点时，△ADQ的面积为1，则?ABCD的面积为（ ）
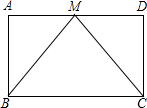已知：如图，在?ABCD中，M是AD的中点，连接BM、CM，且BM=CM，求证：?ABCD是矩形．
在矩形ABCD中，对角线AC与BD交于点O，∠AOB=60°，点E为AD边的中点，AC=8cm，AF⊥BD于点F．求：