题目内容
2.如图,四边形ABCD是平行四边形,E、F、G、H分别是各边的中点,证明图中阴影部分是平行四边形.
分析 ①根据平行四边形的性质可得AD=BC,AD∥BC,再根据中点定义可证明AH=FC,进而可得四边形AHCF是平行四边形;
②与①同理可证明四边形AHCF是平行四边形,进而可得AF∥HC,同理:AG∥EC,根据两组对边分别平行的四边形是平行四边形可得四边形ANCM是平行四边形;
③连接AC,根据三角形中位线定理可得HG∥AC,HG=$\frac{1}{2}$AC,同理可得EF∥AC,EF=$\frac{1}{2}$AC,进而可得EF∥GH,EF=HG,从而可得四边形EHGF是平行四边形.
解答 证明:①∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵H、F是AD和BC中点,
∴AH=$\frac{1}{2}$AD,FC=$\frac{1}{2}$BC,
∴AH=FC,
∴四边形AHCF是平行四边形;
②∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵H、F是AD和BC中点,
∴AH=$\frac{1}{2}$AD,FC=$\frac{1}{2}$BC,
∴AH=FC,
∴四边形AHCF是平行四边形,
∴AF∥HC,
同理:AG∥EC,
∴四边形ANCM是平行四边形;
③连接AC,
∵F、G分别是AD、DC中点,
∴HG∥AC,HG=$\frac{1}{2}$AC,
同理:EF∥AC,EF=$\frac{1}{2}$AC,
∴EF∥GH,EF=HG,
∴四边形EHGF是平行四边形.
点评 此题主要考查了平行四边形的性质和判定,关键是掌握平行四边形对边平行且相等,一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
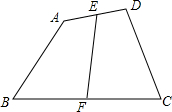 四边形ABCD中,E,F分别为AD,BC的中点,EF=m,则AB+CD的最小值为2m.
四边形ABCD中,E,F分别为AD,BC的中点,EF=m,则AB+CD的最小值为2m.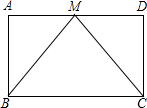 已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.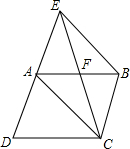 如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?
如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?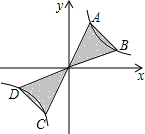 已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.
已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8. 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求: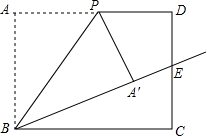 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.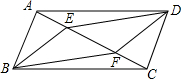 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.