题目内容
5．若关于x的方程x2+kx-12=0与3x2-8x-3k=0有一个公共根，求实数k的所有可能值．分析 根据题意知，当关于x的方程x2+kx-12=0与3x2-8x-3k=0有一个公共根时，构建方程组解决问题即可．
解答 解：时公共根为m，
则有$\left\{\begin{array}{l}{{m}^{2}+km-12=0}\\{3{m}^{2}-8m-3k=0}\end{array}\right.$，
①×3-②得到m=$\frac{36-3k}{3k+8}$代入①化简得到9k3+15k2+504k-528=0
∴（k-1）（9k2+24k+528）=0，
∵9k2+24k+528＞0，
∴k=1．
点评 本题考查了根的判别式．此题也可以将已知的两个方程组成方程组，求出x及k的值即可．
练习册系列答案
相关题目
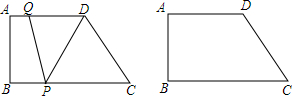
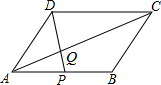如图，在?ABCD中，点P在AB上，连结DP，交AC于点Q，当点P是AB的中点时，△ADQ的面积为1，则?ABCD的面积为（ ）
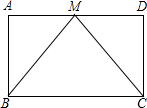已知：如图，在?ABCD中，M是AD的中点，连接BM、CM，且BM=CM，求证：?ABCD是矩形．
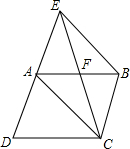如图，已知E为?ABCD的边DA的延长线上的一点，且AE=AD，EC交AB于点F，那么，EF=CF吗？为什么？
在矩形ABCD中，对角线AC与BD交于点O，∠AOB=60°，点E为AD边的中点，AC=8cm，AF⊥BD于点F．求：