题目内容
19.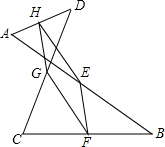 如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.
如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.
分析 首先运用三角形中位线定理可得到HG∥AC、EF∥AC、HE∥BD、GF∥BD,从而在根据平行于同一条直线的两直线平行得到HG∥EF,HE∥GF,即可得出四边形EFGH为平行四边形.
解答 解:四边形EFGH为平行四边形,理由如下: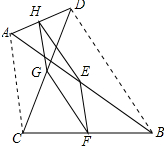
连接AC、BD,如图所示:
∵E、F、G、H分别是线段AB、CB、CD、AD的中点,
∴HG为△DAC的中位线、EF为△BAC的中位线、HE为△ABD的中位线、GF为△CBD的中位线,
∴HG∥AC,EF∥AC,HE∥BD,GF∥BD,
∴HG∥EF,HE∥GF,
∴四边形EFGH为平行四边形.
点评 此题主要考查了三角形中位线定理、平行线的判定、平行四边形的判定等知识,熟练掌握三角形中位线定理与平行于同一条直线的两直线平行是解决问题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.
如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.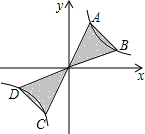 已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.
已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8. 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求: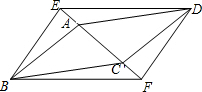 如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.
如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.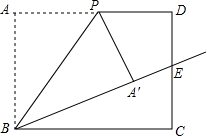 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.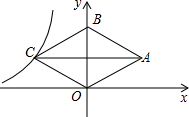 如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.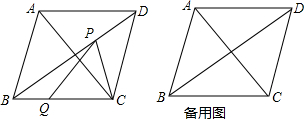 如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)
如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)